Természetes logaritmus tulajdonságai, grafika és funkció

Lecke és prezentációs témák: „a természetes logaritmus alapja a természetes logaritmus logaritmus természetes szám ..”

Mi a természetes logaritmus

Srácok, az utolsó leckét fogunk tanulni az új, különleges szám - e. Ma folytatja a munkát ezzel a számmal.
Mindannyian tanult a logaritmus és tudjuk, hogy az alapja a napló lehet számsor, amely nagyobb, mint 0. Ma is nézd meg a log, az alap az, amely a számos e. Ez a napló az úgynevezett természetes logaritmus. Ő a saját rekord: $ \ ln $ - természetes logaritmus. Ez a bejegyzés megegyezik a felvétel: $ \ log_e = \ ln $.
Exponenciális és logaritmikus függvények fordított, akkor a természetes logaritmusa az inverz függvény: $ y = e ^ x $.
Inverz függvények szimmetrikus vonal $ y = x $.
Építsünk egy grafikon, a természetes logaritmus, tükrözve az exponenciális függvény képest egy egyenes vonal $ y = x $.

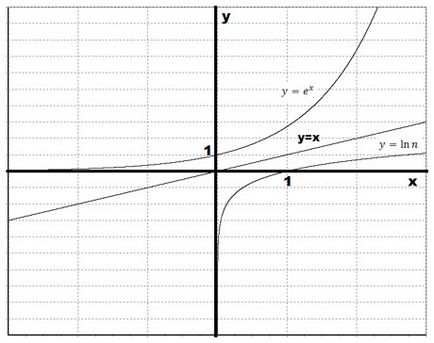
Érdemes megjegyezni, a dőlésszög az érintő a grafikon a $ y = e ^ x $ pontnál (0, 1) a 45 °. Ezután a dőlésszög az érintő a grafikon a természetes logaritmusa pont (1; 0) is egyenlő 45 °. Mindkét érintők párhuzamos vonal $ y = x $. Nézzük vázlatosan ábrázolja a tangens:

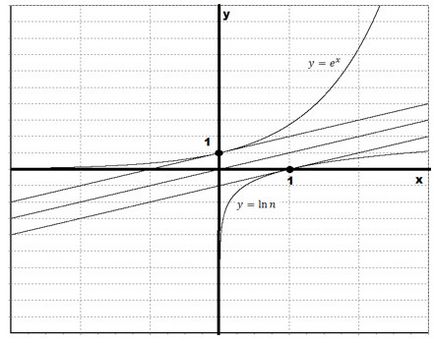
Tulajdonságok A függvény $ y = \ ln $

1. $ D (f) = (0; + ∞) $.
2. Van olyan páros vagy páratlan.
3. Növekedés a teljes domaint.
4. Ne korlátos fent említett, nem alulról korlátos.
5. A legnagyobb érték nincs jelen, a legalacsonyabb érték van.
6. folyamatosan.
7. $ E (f) = (- ∞; + ∞) $.
8. A felfelé domború.
9. differenciálható mindenhol.

A természetesen Matematika bebizonyította, hogy a származék az inverz függvény az inverze a függvény deriváltját.
Ásni a bizonyítékok nem sok értelme, nézzük csak írni a képlet: $ y „= (\ ln)” = \ frac $.

Példa.
Számítsuk ki a értéke differenciálhányados: $ y = \ ln (2x-7) egy ponton $ x $ 4 = $.
Határozat.
Általánosságban elmondható, hogy a funkció függvénye $ y = f (kx + m) $, ezek származékai funkciókat tudjuk számolni.
$ Y '= (\ ln)' = \ frac $.
Kiszámoljuk a értéke a származék a kívánt ponton: $ y „(4) = \ frac = $ 2.
Válasz: 2.

Példa.
A érintő a grafikon a $ y = ln $ $ x pontban = e $.
Határozat.
Az egyenlet az érintő a függvény grafikonját a ponton $ x = a $, emlékszünk.
$ Y = f (a) + F „(a) (x-a) $.
Egymást követően kiszámítja a szükséges értékeket.
$ A = e $.
$ F (a) = f (e) = \ ln = 1 $.
$ F „(a) = \ frac = \ frac $.
$ Y = 1 + \ frac (X-e) = 1 + \ Frac \ frac = \ frac $.
Az egyenlet az érintő ponton x = e $ $ függvénye $ y = \ frac $.
Építsünk egy grafikon a természetes logaritmus és az érintő.

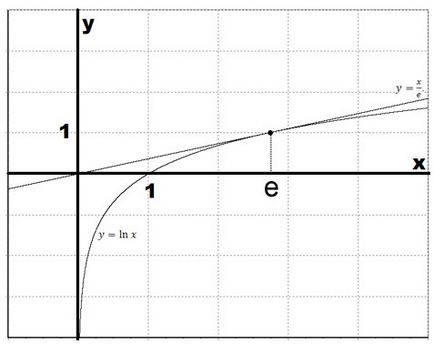
Példa.
Fedezze fel a funkciót a monotonitást és szélsőséges: $ y = x ^ 6-6 * ln $.
Határozat.
A domain a funkció $ D (y) = (0; + ∞) $.
Keressük a származék egy adott funkció:
$ Y „= 6 * x ^ 5- \ frac $.
Származtatott létezik az összes x a tartomány meghatározása, akkor nincs kritikus pontokat. Mi található a stacionárius pontok:
$ 6 * x ^ 5- \ frac = 0 $.
$ \ Frac = 0 $.
$ 6 * x ^ 6-6 = 0 $.
$ X ^ 6-1 = 0 $.
$ X ^ 6 = $ 1.
$ X = ± 1 $.
X = -1 $ $ nem tartozik a domain meghatározása. Aztán van egy fix pont $ x = 1 $. Találunk szüneteiben növekedése és csökkenése:

Point $ x = 1 $ - minimum pont, akkor a $ y_min = 1-6 * \ ln = 1 $.
A: A funkció csökken az intervallum (0, 1], a funkció növeli ray $ [1; + ∞) $. $ Y_min = 1 $.

Srácok, ki tudjuk számítani a származékok a természetes logaritmus és exponenciális függvények. De nem tudjuk, hogyan kell kiszámítani a származékos logaritmusának más vagy az exponenciális függvény.
Tekintsük az exponenciális függvény $ y = a ^ x $.
Emlékezzünk az ingatlan: $ c ^> = b $.
Aztán: $ a = e ^ $.
$ A ^ x =)> ^ x = e ^ $.
Keressük a származék: $ (a ^ x) '= (e ^)' = \ ln * e ^ = \ ln * a ^ x $.
A származék az exponenciális függvény: $ (a ^ x) „= \ ln * a ^ x $.

Mi jár a logaritmusok használjuk a képlet átmenetet egy új bázis:
$ \ Log_a = \ frac> $.
Keressük a származék: $ (\ log_a) '= (\ frac>)' = \ frac * (\ ln) „= \ frac * \ frac = \ frac $.
A származékot alapú logaritmusa és a szám x egyenlő:
$ (\ Log_a) „= \ frac $.

Kihívások a természetes logaritmus önrendelkezésért

1. Számítsuk ki a értéke differenciálhányados $ y = \ ln $ azon a ponton, x = $ 3 $.
2. Számítsuk ki az érték a differenciálhányados $ y = \ log_4 $ azon a ponton, x = $ -2 $.
3. Keresse meg az egyenlet érintő a grafikon $ y = \ ln $ a $ x = $ 2e. Sematikusan ábrázolják egy grafikont.
4. Megvizsgálni a funkciót a monotonitást és véglet: $ y = x ^ 8-4 * \ ln $.