Lineáris regresszió példákkal r, programozás, algoritmusok, és nem csak
Régóta folytatja azt az elképzelést, séta a legfontosabb algoritmusok adatbányászat. rendszerezése a meglévő ismeretek és értékelést készít a példákat. Tulajdonképpen ez a cikk, és lesz az elején a sorozat. Például akkor használható szoftver környezet R. amiről írtam egy előző post.
lineáris regresszió
Szigorúan véve, a lineáris regresszió algoritmus nem adatbányászat. Ez az egyik módszer származik statisztika. A statisztikában a regresszió általában azt jelenti, jóslat, egy vagy más formában. Sok különböző típusú regresszió, de az alapján, ezek közül bármelyik egy és ugyanaz a gondolat: építeni egy modellt, amely kapcsolódik a várható érték a forrás adatok (előrejelzője), minimalizálva hiba.
Lineáris regresszió a legegyszerűbb változata regresszió. Vegyük például, lineáris regresszió egy prediktor és egy előre jelzett értéket. Ez regresszió könnyű felhívni az X-Y gráf. Ehhez a vízszintes tengelyen az X, tudomásul vesszük értékét előrejelzője, és az ordináta Y értékek a várható érték. Ezután az egyszerű lineáris regresszió húzott vonal oly módon, hogy minimálisra csökkentse a különbséget a valódi értékek és a becsült értékek a pontokat a megfelelő sorban értékeinek előrejelzője.
A matematika nyelvén, le tudjuk írni a lineáris modell formájában az egyenlet: Y = a + b * X, ahol X - előrejelzője vagy a nyers adatokat, és Y - az előrejelzett érték. A maga feladata átfogalmazni: megtalálni a és b együtthatók minimalizálása a hiba értékét.
Ha a modell épül, és az együtthatók találhatók, fel tudjuk használni a kapott egyenlet megjósolni ismeretlen értékek számunkra.
Vegyünk egy példát a pénzügyek területén. Nem titok, hogy a tőzsdei árfolyamok olajtársaságok erősen függnek az olajárak. A nulla közelítés, akkor feltételezhetjük, hogy
A részvényárfolyam = K * Az ár egy hordó olaj + egy bizonyos állandó
Ha meg tudjuk határozni egy állandó tényezőt, majd tudjuk megjósolni az olaj ára részvényárfolyam. Ha van eltérés, akkor vegyél egy terjedése és a pénzt, elméletben, természetesen.
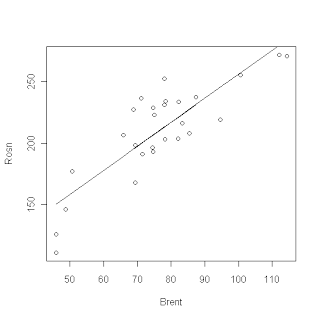
És most a gyakorlatban, hogy az R, és felhívni a lineáris regresszió a cég Rosneft olaj ára áron. Az eredeti adatok megtalálhatók itt:
eredmény:
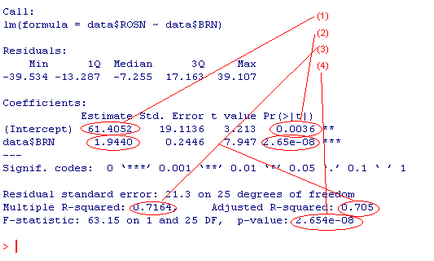
Az ábrán, mi érdeke aránya jelzi (1). Behelyettesítve őket a regressziós egyenlet, megkapjuk a kifejezést: ROSN = 61,405 + 1,944 * Brent mellett értékek ténylegesen együtthatók R megmutatja a mennyiségét hibák, vagy a standard eltérést az egyes együttható. De ez még nem minden. Például előfordulhat, hogy vajon ez semmit megmagyarázni mi áron. Ennek tesztelésére is előadott a nullhipotézist, hogy például az együttható 61405 csak az eredmény a hiba, és ennek értéke elhanyagolható. A hipotézis, a Student-féle t-teszt. Itt R nekünk mindent megtesz a munkát, értékének kiszámításánál is, mint a t és mértékének jelentőségét hipotézisünk Pr (> | t |). Tehát a mi esetünkben az érték (2) 0,0036 azt jelenti, hogy mi vagyunk a 100 * (1-0,0036) = 99,64% úgy véli, hogy az állandó kifejezés ez a kifejezés nem nulla. Ezután tudjuk ellenőrizni, hogy mennyire jól modell leírja az adatokat. Ebből a célból, az együtthatók R2 (3). Minél közelebb ezeket az értékeket az 1 értéket, annál jobb. 1 ideális eredmény, ami azt jelenti, hogy 100% -os modell írja le az adatokat. És végül, az utolsó dolog, amit ellenőrizni is, hogy a várható érték függ a előrejelzője. Ehhez a nullhipotézist felhozott, hogy a várható érték nem függ prediktorainak. Ennek a hipotézisnek határoztuk p-érték (4). A mi esetünkben azt találtuk, hogy 2,65 * 10 ^ -8. Ie biztosak lehetünk abban, hogy 99.99999735%, ami a várható érték tényleg attól függ, előrejelzője. Általában akkor van értelme, hogy nézd meg ezt a lehetőséget, az első helyen, mert ez határozza meg, milyen általános modellünk megfelelő. Ja, és egy kis fenti grafikon, csak azt mutatja, adataink és az eredmény a lineáris regresszió.
Mi történik, ha az adatok nem írja le egy egyenes vonal?
Lineáris regresszió egyik előrejelzője a legegyszerűbb változata a regresszió, a gyakorlatban számos lehetséges szövődmények amely megoldja sokkal összetettebb probléma: 1) számos kiegészítő előrejelzője - további előrejelzője további információkat adhat hozzá a modell, és így a túlélést. Az egyenlet a lineáris regressziós ezután a következő formában: Y = a + b1 * X1 + ... bn * Xn 2) előzetes transzformációs előrejelzője - építése becsléséhez fokozat vagy gyökerek extrakciós egyik módja, hogy növelje a lehetőségét lineáris regresszió. A gyakorlatban gyakran van szükség, hogy végezzen számos különböző átalakulások érdekében, hogy melyik közülük fog adni a legjobb becslés. 3) az egyenletben a modell lehet hozzáadni a terméket tartalmazó tag előrejelzője 4) gyakran felmerül a probléma előre a valószínűségét egy esemény. Ie előrejelzett érték mindössze két érték 1 vagy 0, és igen és nem. Az ilyen problémák megoldására használják logisztikus regresszió. Szerencsére, ezek és még sok más kiegészítéseket R és használatra kész. Arról, hogy hogyan kell használni őket megtalálható gépelni a parancs interfész R.
Serge San Francisco, Kalifornia, Egyesült Államok Szia, én vagyok a vezető szoftvermérnök egy nagy webes cég. Főként az érdekli adatbányászati és gépi tanulás. Saját „bennszülött” programozási nyelv a Java, de úgy vélem, Haskell és FP általában jobb. Van tisztességes tapasztalat C # és .NET stack is. Szabadidőmben Örülök, hogy versenyezni okos emberek TopCoder és Kaggle. Saját TC profil van. Kaggle profil ide Ha akar beszélni, csak küld egy üzenetet: e d u n o v @ g m i b. c o m Teljes profil megtekintése