amper törvénye
Az irány az amper erő
Amp előbb megállapította, hogy a vezetékek, amelyek az elektromos áram kölcsönhatásba mechanikusan (vonzzák vagy taszítják). Erő ($ \ overrightarrow $), ami hatással van az egyenes huzal hordozó áram (I), és a karmester mindig merőleges a mágneses indukció vektor ($ \ $ overrightarrow). Ebben az esetben egy egyenes vonalú útmutató párhuzamosan elhelyezett mentén a mágneses erővonalak, a mező nem érvényes. A konkrét iránya Amper erő megtalálható a bal kéz szabályt. A bal kéz úgy kell elhelyezni, hogy a mező vonalak szerepelnek a kéz, négy ujj már irányított áram, majd a hajlított 90 fokos szögben a hüvelykujjával jelzi az irányt a amper erő. Ha az irányt a vektor $ \ $ overrightarrow szöget zár az irányt a jelenlegi, célszerű, hogy elterjedt a mágneses indukció vektor két komponensre (1. ábra), hogy meghatározzuk az irányt az erő Amper:
ahol $ \ overrightarrow> $ - merőleges a jelenlegi, $ \ overrightarrow> $ - párhuzamosan a jelenlegi. Csak $ \ overrightarrow> $ - okozza a hatás a területen, akkor kell alkalmazni a szabályt, a bal kezét.
Problémák kontroll minden tantárgyból. 10 éves tapasztalat! Ár 100 rubelt. 1-jétől nap!
Írunk az olcsó és éppen időben! Több mint 50 000 bizonyított szakemberek
Különleges ajánlat! Ily módon 100 rubelt.
elsőrendű!
200 rubel / 2 óra
350 rubel / 2 óra
50 rubel / 2 óra
Több Amper találta, hogy két, egymással párhuzamos, a felvett áram, ha az áramok azonos irányban, és taszítják, amikor áramok egymással ellentétes irányban. Ez könnyű megmagyarázni, ha azt képzeled, hogy egy vezető mágneses mezőt hoz létre, és a többi vezető kerül, és ezen a területen jár rajta. Akkor használja a bal kéz szabály, és hogy megtudja, hogyan az erő irányul.
Ampere törvénye
Lineáris vezeték Amper erő a következő:
ahol a $ I $ - aktuális, ami folyik a vezetőben, $ \ overrightarrow $ - vektor mágneses mezőt, amelyben a vezető kerül, $ \ overrightarrow $ - vezetékhossz irányban meg van adva, az irányt a jelenlegi. amper tápegység ebben az esetben:
Nyilvánvaló, hogy a gyakorlatban nem minden vezeték egyenesek. Azonban bármely vezeték lehet osztani több részből, amelyeket figyelembe kell venni, egyenes. Aztán a koncepció az aktuális elem - az az összeg egyenlő $: \ Id \ overrightarrow $, ahol $ d \ overrightarrow $ - elemi egyenes szakasz a karmester, a vektor irányított aktuális. Akkor Ampere törvénye van írva a következő:
A skalár formában (4) felírható:
ahol $ \ alpha $ - közötti szög vektorok $ \ overrightarrowi \ \ $ overrightarrow.
Amper ható erő huzal jelenlegi véges hosszúságú lehet összeadásával a (vektor):
ahol az integrálást végezzük teljes hossza mentén, a karmester.
Kifejezések (2) és (4) - Amper törvénye.
Mert párhuzamos, végtelen hosszú áram amper erő a formája:
ahol a $ I_1, I_2 $ - az áramokat a vezetékek, $ d $ - közötti távolság a vezetékek, $ l $ - vezetékhossz $ (l \ gg d) $, $ _0 = 4 \ pi \ cdot ^ \ frac \ (Henry \ to \ m) $ mágneses állandó. Ez a képlet könnyen nyert a törvény amper.
Ha az egyik vezeték nem egyszerű, és meg kell találnunk a Amper erő, amely rajta. A mező ugyanakkor létrehoz egy hosszú, egyenes vezető. Ezután, a kívánt hatás megtalálható képlet alapján:
ahol a $ df $ - Amper ható elemi áramvezető ($ I_2 \ overrightarrow $) egy végtelen hosszú egyenes vezető egy jelenlegi $ I_1 $.
Az érték Ampere törvénye
A törvény alapján az amper van beállítva jelenlegi SI egységek és emu rendszereket. Mivel amper egyenlő az egyenáram, amely, amikor mentén áramló két párhuzamos végtelen hosszú, egyenes vezetékek a végtelenül kicsi kör keresztmetszetű, egy 1 m távolságra egymástól vákuumban okoz a kölcsönhatás erőssége Ezen vezetékek egyenlő $ 2 \ cdot ^ N $ méterenként.
Cél: Egy mágneses mező függőlegesen lefelé két súlytalan szálak vízszintesen felfüggesztett-áram erőssége I = 2A. Mass vezeték $ m = 10 ^ $ kg, hossza L = 0,4 m. mágneses mező indukció 0,25Tl. Határozzuk meg a szöget, amelyek megváltoztatják a fonalat, amelyen lóg egy áramvezető. Vezényel minden területén.
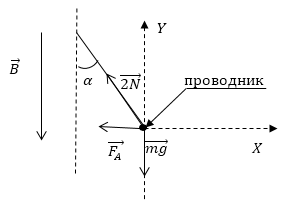
A karmester van elhelyezve, merőlegesen a rajz síkjára (elfelé a jelenlegi velünk). Írunk az egyensúlyi állapot a karmester:
ahol $ \ overrightarrow $ - Amper, $ \ overrightarrow $ - gravitáció, $ \ overrightarrow $ - reakció erő menet.
Tervezés (1.1) a tengely:
\ [X: \ -F_A-2Nsin \ alpha = 0 \ \ left (1,2 \ right) \.] \ [Y: \ Mg + 2Ncos \ alpha = 0 \ \ left (1,3 \ right) \.]
Osztjuk (1.2) a (1.3), kapjuk:
Amper tápegység modul lineáris vezetőn áram felfüggesztett egy olyan területen, a jelenlegi, és a $ \ overrightarrow \ bot \ overrightarrow \ $ jelentése:
Átírjuk (1.4) és (1.5), kapjuk:
Behelyettesítve eredeti adatokat fog végezni számítások:
Válasz: $ \ alpha \ kb 64<>^ \ Circ $.
Feladat: A áramvezető van egy négyzet alakú, akkor elfolyik a jelenlegi I. egy síkban a keret egy végtelenül hosszú, egyenes vezető azonos áram. Elhelyezkedés vezetékek a 3. ábrán. Keresse mekkora erővel hat a keret, ha a távolság az egyik oldalon a keret és vezeték hosszával megegyező a térre.
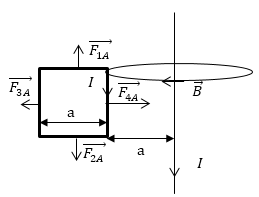
A mágneses mező által generált végtelen hosszú vezeték. A modul a mező indukció tudjuk felírható:
ahol r - palacsinta-re a vezetőt a területen pont.
Field huzal egy hengeres szimmetria, minden túlmutat ez merőlegesen. Ha figyelembe vesszük, viszont Amper ható erő mind a négy összetevője a keret, a kifejezés az Ampere erő a modul használható formában:
ahol $ l = $ a. Meg kell jegyezni, hogy az oldalán, amelyek merőlegesek az áramvezető jár erő egyenlő nagyságú és ellentétes irányú, így a kapott a hozzájárulás nulla. $ \ Overrightarrow> $ = - $ \ overrightarrow> $.
Force $ F_ \ és \ $ F_ mentén vannak ugyanazon a vonalon, de ellentétes irányban. Következésképpen, az eredő erő a modul található, mint:
Segítségével Ampere törvénye, és szem előtt tartva, hogy a mágneses mező merőleges a jelenlegi oldalán a tér, írhatunk:
Behelyettesítve (2,5) a (2.4), kapjuk: