Megfelelő (rezonáns) frekvencia állóhullámok
A gyakorlatban, abban az esetben szabad rezgés bizonyos fizikai rendszerek, mint például a húr, stb oszlopok gáz. Állóhullámok be van állítva, a gyakoriságát, amelyek megfelelnek bizonyos feltételeknek, azaz a. E. May hogy csak bizonyos diszkrét értékek, az úgynevezett természetes frekvenciáit a rezgő rendszer.
Például, a pontok rögzítő húrok vagy rudak eltolva vannak elrendezve csomópontok (amplitúdópont törzsek), míg a szabad végei a rudak amplitúdópont elmozdulás (alakváltozás csomópontok). Amikor levegőrezgések oszlop egy hengeres csövet a zárt végén a cső elhelyezkedik, nyomásváltozás amplitúdópont, és a kültéri egység nyomás. Példaként, előfordulását vizsgáljuk állóhullámok a rezgő húr feszültség változások (parametrikus rezonancia). Frekvencia állóhullámok nevezzük belső, vagy rezonancia. t. Hogy. Az ilyen rezgések kíséri a rezonancia jelenség. Ellentétben tavasz, matematikai vagy fizikai ingával, amelyben a rezgések egy természetes rezonancia frekvencia (egy szabadsági foka), a feszes húr sok frekvenciáknál.
Ezek a frekvenciák viszont többszöröse a legalacsonyabb frekvencia.
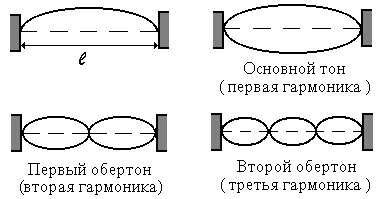
Hosszú idő alatt a hullámok vannak tárolva, amely megfelel a rezonancia frekvenciát. A rögzítési pontok a bitsorozatot, amelynek csomópontok (ábra. 4.7). Ahhoz, hogy megtalálja a sajátfrekvenciáira használatának az a tény, hogy a hossza az állóhullám kapcsolódó húr hossza:
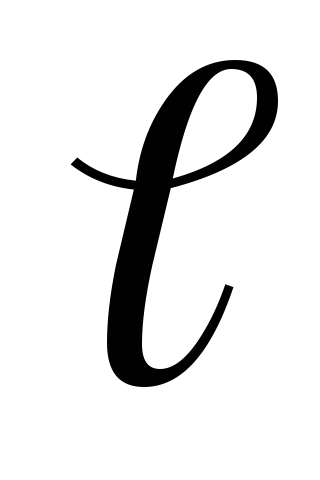
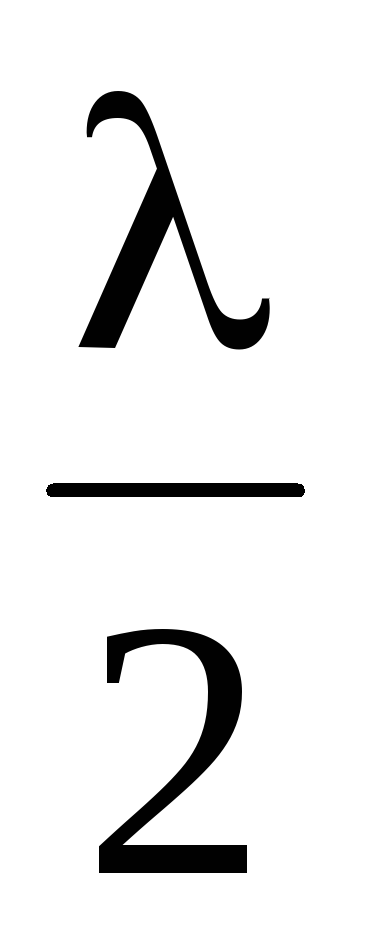
Például az alapvető hang (divat) első harmonikus megfelel a amplitúdópont és a hossza a húr
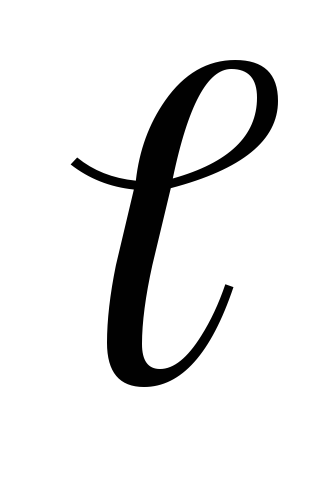
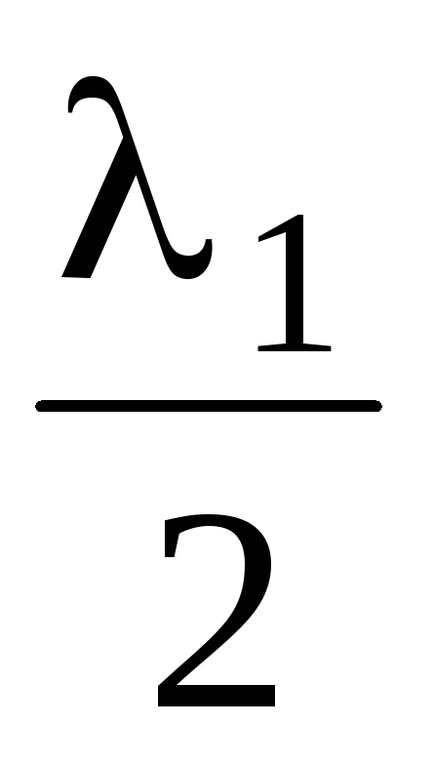
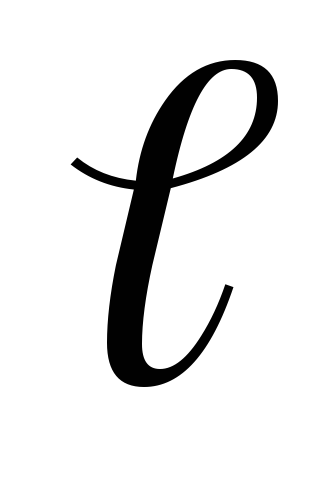
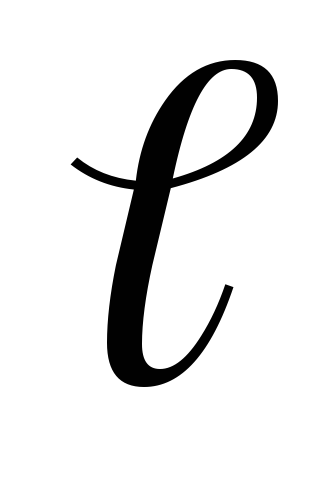
Megjegyzés: Az állóhullám létezhet csak szigorúan meghatározva rezgési frekvenciáját.
Valóban, állapotának megfelelően az hiányában rezgések a jobb oldali végén egy rögzített karakterlánc, ahol a koordináta X =
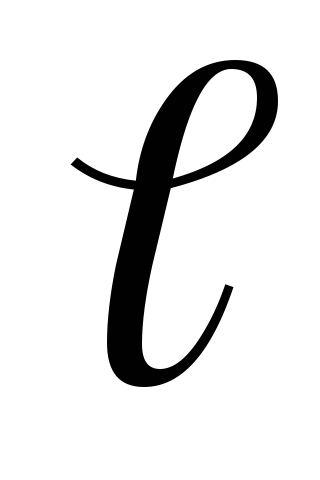
Ast = 2Acos (kx
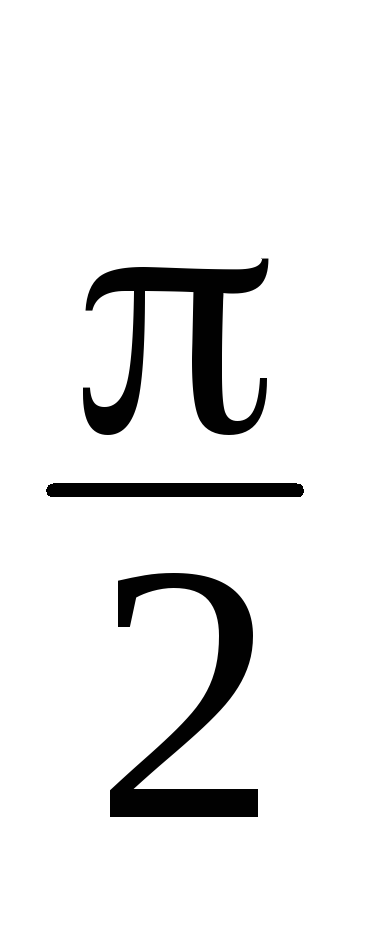
A pontokon, ahol sin (kx) = 0, nem lesz csomópontok és sin (k
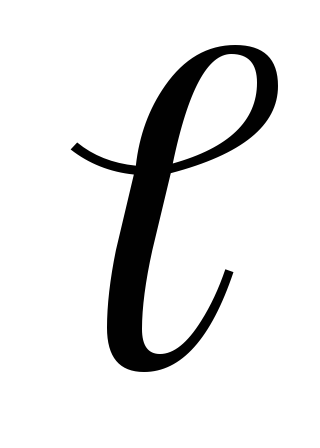
Általános következtetés: Az eredmény szokatlan klasszikus fizika mert k hozhat szigorúan meghatározott értékek:
A megfigyelt rendellenesség igen jelentős hatást gyakorol a válasz kvantum jelenségek.
Megállapításai szerint a kvantumelmélet, hogy minden microobjects rendelkeznek korpuszkuláris és a hullám tulajdonságait.
4.12. Akusztikus Doppler-effektus
Ha egy rögzített oszcilláló forrást, egy álló közeg és egy fix frekvencia vevő sugárzott elosztott és vett hullámok egyenlő.
Más a helyzet, ha azokat mozgásba, t. E. A változás a frekvencia a felvett hullámok.
A frekvencia-ingadozások miatt hullámmozgás rezgésforrás és a vevő az úgynevezett Doppler-effektus.
Nézzük az egyes eseteket, amikor a forrás mozog (közeledik udalyaetsya) vagy vevő (priblizhaetsyaudalyaetsya), vagy mindkettő (priblizhayutsyaudalyayutsya).