Határozott integrál és szerves összegek, 3. oldal

Vegye figyelembe, hogy a geometriai jelentése a határozott integrál

Ezt szem előtt tartva, megkapjuk az első értékelés a határozott integrál.

8. tulajdonság (a középérték-tétel). Ha az f (x) folytonos a [a, b], majd ebben az intervallumban van egy olyan pont, hogy, hogy a következő egyenlőség:

Megjegyezzük, hogy a geometriai átlag érték tétel azt jelenti, hogy a terület a trapéz ívelt területe egy téglalap oldalai F (a) és (b-a). Ezért ez a tétel nagy elméleti jelentősége igazolására numerikus integrálási módszerek, mert alapvetően a fő célja ezeknek a módszereknek a lehető legpontosabban kell választani a pontot.

3.4. Hozzávetőleges módszerek határozott integrálok

Közelítő számítási módszerek határozott integrálok van azon a tényen alapul, hogy a határozott integrál lehet tekinteni, mint a terület az íves trapéz. A terület trapéz lehet számítani, ha a helyébe egyszerűbb alak: az összeg a téglalapok, trapéz, vagy más figura. A gyakorlati jelentősége az ilyen módszerek, hogy pontosan kiszámítani a határozott integrál nem mindig lehetséges. Ezen túlmenően, az integrandus gyakran adják táblázatos vagy grafikus formában. csak közelítő módszereket lehet használni ezekben az esetekben. Megnézzük ketten - a módszer a téglalap és a trapéz módszer.

3.4.1. téglalap módszer

Osszuk az integráció [a, b] n egyenlő részre a pontok:

ahol h = (b-a) / n - integráció lépésben. Mi cserélni ezt ívelt lépett trapéz alakja álló N yaschey téglalapok (lásd. Ábra. 3.2). Az érték a terület a szám, és ad egy közelítése a kívánt integrál:

A kapott expressziós nevezett képletű téglalapok.

Amint ci lehet választani, mint a bal oldali (ci = xi-1) és a jobb (ci = xi) határait a partíció részek. Ebben az esetben az ívelt területe trapéz nagyjából megegyezik a területek összege, vagy a bal vagy a jobb a téglalapok. Módszerek jobb és bal oldali téglalapok ad közelítése a határozott integrál precíziós arányos integrációs h lépés. Sőt, az egyik módszer ad szerves értéke meghaladja, és a másik egy hátránya. Ezért, mint a pontos értéket az integrál vehet a számtani átlaga mindkét módszer, míg a köztük lévő különbség ad egy hiba kiszámítása. Egy ilyen eljárás már úgy a 3.1 példában.

Általában az eljárás a téglalapok érteni esetben, ha például a pontok ci vett közepe particionálás részek, azaz a ci = (xi-1 + xi) / 2. Ebben az esetben, a hiba kiszámítására a határozott integrál arányos h 2. azaz egy nagyságrenddel nagyobb, mint a módszerek a balra vagy jobbra a téglalapok.

3.2 példa. Keresse meg a képletét téglalap közelítő értéke az integrál

Határozat. Osszuk a [0; 1] 10 egyenlő részre. Találunk minden egyes szegmense ci és a középső érték a függvény ezeken a pontokon. Létrehoztunk egy táblázatot

A hiba körülbelül 0,0004.

3.4.2. A trapéz módszer

A második legegyszerűbb módja annak, hogy közelítő kiszámítása határozott integrálok a trapezoid módszer, amely abban a tényben rejlik, hogy a függőleges csíkok nem váltják fel téglalapok, és trapéz. Más szóval, a grafikon az f (x) függvény helyébe sokszög vonal (lásd. Ábra. 3.5).

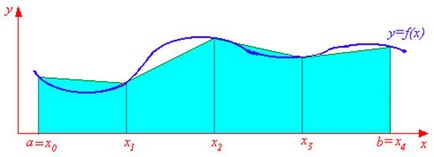
Ennek eredményeként a terület a teljes alak áll négyzetek lineáris trapéz szabály. A terület egyes trapéz a termék egy fél-összeget a bázisok a magassága:

ahol yi = f (xi). Ezután a trapéz kvadratúra- képlet fog kinézni

Figyeljük meg, hogy a hiba határozza numerikus integrálással lépés integrálása, a trapéz módszer hibája is arányos h 2. csökkentése integrációs lépés lehet elérni nagy pontossággal.

3.3 példa. Keresse trapéz közelítő értéke az integrál

Határozat. Osszuk a [0; 1] 10 egyenlő részre. Minden ponton, azt látjuk, a függvény értékét. Létrehoztunk egy táblázatot

Pontosság is megközelítőleg 0,0004.

KÉRDÉSEK SELF

1. Hogyan készülnek szerves összegeket?

2. Van-e a halmozott összeget a módszer felosztása a szegmens? kiválasztásának módszere a közbenső pontok?

3. Mi a határozott integrál? Mi ez alapvetően különbözik a bizonytalan?

4. Vajon a határozott integrál módszer megosztottság a szegmens? kiválasztásának módszere a közbenső pontok?

5. Adjon és bizonyítani lineáris tulajdonsága határozott integrálok?

6. Fogalmazza meg a tulajdonságait a határozott integrál, nem jellemző határozatlan integrálok?

7. Ismertesse a módszer téglalapok numerikus számítási határozott integrálok?

8. Ismertesse a trapéz módszer numerikus számítási határozott integrálok?

Gyakorlatok és feladatok

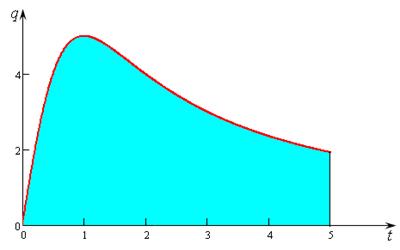
1. Legyen a függőség az értékesítési volumen a termék az idő által meghatározott funkciót

Ezután, értékesítési területet Q árnyékolt ábra (3.6 ábra), azaz a ismét, a terület a görbe vonalú trapéz, és tudjuk alkalmazni ugyanazt a módszert a kimerültség, hogy hozzávetőleges meghatározása a módszer a kimerültség Q. Számítsuk területe a görbe vonalú trapéz Q.

2. Számítsuk ki a képletek téglalapok és trapézok n = 10 integrálok

3. Keresse meg a maximális érték a beépített funkció az összeget a szegmens
[0; 1], ha a szegmensek száma 4 partíció.

4. kiszámítása nélkül integrálok, megtudja, melyik az integrálok át: