Bernoulli lemniscate

Az elnevezés az ókori görög. λημνίσκος - szalag kötést. Az ókori Görögországban „mozgató”, az úgynevezett íj, segítségével, amely csatlakozik egy koszorút a fejét a győztes atlétikai játékokat. Ez a típus lemniscate nevezték a svájci matematikus Jacob Bernoulli. ez volt az a kísérlet kezdetén.

Tekintsük a legegyszerűbb esetet: ha a távolság a gócok 2 c. azok helyét a tengelyen O X. és a származási osztja közötti szegmenst a két fél, a következő egyenletek határozzák meg a lemniszkáta:

Foci lemniszkáta - F 1 (- c 0) (-c; 0)> és F 2 (c 0) (c; 0)>. Vegyük bármely ponton M (x; y). A termék a távolságok gócok a pont M

és definíció, ez egyenlő c 2>:

Kihúzta mindkét oldalon:

Nyilvánosságra zárójelben a bal oldalon:

Leleplezése konzolok és tekerjük fel az új összegének négyzetével:

Mi vegye ki a közös tényező, és húzza:

Akkor lehet, hogy a változás a 2 2 = c 2 = 2c ^>. bár ez nem szükséges:

Ebben az esetben a - a kör sugarát leíró lemniscate.

Miután egyszerű átalakulás egy kaphatnak explicit egyenletet használva: y = ± C 4 + c 2 x 4 2 - x 2 - c 2 + 4x ^ c ^ >> - x ^ -C ^ >>>

Kihúzta és nyilvánosságra zárójelben:

Az űrlap

Figyelembe a gyökér és eldobjuk a kiviteli alakban egy negatív második kifejezés, kapjuk:

ahol pozitív opció határozza meg a felső fele a mozgató, negatív - alacsonyabb.

(Ρ 2 cos 2 ⁡ φ + ρ 2 sin 2 ⁡ φ) 2 = 2 c 2 (ρ 2 cos 2 ⁡ φ - ρ 2 sin 2 ⁡ φ) \ rho ^ \ cos ^ \ varphi + \ rho ^ \ sin ^ \ varphi ^ = 2c ^ \ ^ Rho \ cos ^ \ varphi - \ Rho ^ \ sin ^ \ varphi>

Az általunk használt még egy identitás: cos 2 ⁡ α - sin 2 ⁡ α = c o s 2 α \ alpha - \ sin ^ \ alpha = cos2 \ alpha>:

Mint abban az esetben egy négyszögletes rendszer helyettesíthető egy 2 2 = C 2 = 2c ^>:

A sűrűsége a pontokat a görbe egyenletes változása a paraméter

Ez az egyetlen ésszerű lehetőség paraméterezése a görbe. Az egyenlet teljesen görbe írja le, ha a paraméter végigfut az egész számegyenesen. - ∞ és a + ∞. Ebben az esetben, ha a paraméter hajlamos - ∞. pont a görbe hajlamos (0, 0) koordinátája a második negyedévben. és, ha a paraméter hajlamos + ∞. akkor - a negyedik. A pontok elosztására amely a függvény, a változás a paraméter fix pitch látható.

Lemniscate egyenlet poláris

helyettesítő képletben átmenet poláris koordinátái x = ρ cos ⁡ φ. y = ρ sin ⁡ φ. emelt a téren:

Tekintsük az első egyenletből:

x 2 = C 2 2 2 cos ⁡ φ cos 2 ⁡ φ = 2c ^ \ cos 2 \ varphi \ cos ^ \ varphi>

Fogadás a gyökere mindkét oldalán a következő egyenletet:

Ha cserélni p 2 = tg ⁡ (π 4 - φ) = \ operatorname \ left (> - \ varphi \ right)>. megkapjuk a kívánt expressziós x:

Beállításához lemniscate két tetszőleges pontot, akkor nem jelenik meg az egyenletet újra, és határozza meg a koordináta transzformáció, amelyben a régi (jelenleg) a gyújtótávolság halad egy új, és dolgozni az egyenlet által bemutatott ez az átalakulás.

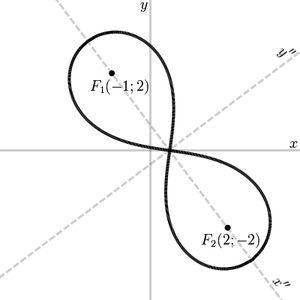
Tegyük fel például, F 1 (- 1; 2). F 2 (2 - 2) (1, 2), \, F_ (2; -2)> - gócok.

Van egy derékszögű koordináta-rendszert (az ábrán - x „O y”), amelyben az egyenlet a forma lemniszkáta

Meg kell határozni egy koordináta-transzformációs rendszer átalakítja x O y és x „O y”. Ezt az átalakítást két lépésben végezzük: a párhuzamos és forgató.

Miután a koordinátarendszer át kell forgatni egy bizonyos szögben. A szög először megtalálni a távolság a gócok:

Most, a geometriai megfontolások találni szinusz és koszinusz a dőlésszög F 1 F 2 F_> O X:

Kombinálásával két transzformáció, megkapjuk a végső transzformációs képletek:

Annak érdekében, hogy egy egyenlet a standard koordinátarendszerben behelyettesítjük az egyenletek az eredeti egyenlet görbe:

x 4 + y 4 + 24 xy - 2 xy 2 + y 2 2 x 2 - 2 x 3 + x 5 x 24 - 2 y 3 - Y 12 + 15 16 = 0 + y ^ + 24xy-2xy ^ + 2x ^ y ^ -2x ^ + 5x ^ -4x-3y ^ -12y +> = 0>

Ez az egyenlet határozza lemniszkáta a gócok F 1 (- 1; 2). F 2 (2 - 2) (1, 2), \, F_ (2; -2)> standard derékszögű koordináta-rendszert.

A secants (Maclaurin módszer)

Construct sugarú kör c 2 >>> középpontja az egyik fókusz. O a középső gyújtótávolság konstrukció tetszőleges szekáns O P S (P és S - a metszéspont a kör), és rajta vannak mindkét oldalára felhordható, a szegmensek O M 1> és O M 2>. egyenlő akkord P S. M pont 1>. M 2> vannak különböző hurkokat a lemniszkáta.

csuklós módszerek

lehetőség One

A sík kiválasztott két pont - A és B - jövő lemniscate gócok. Ez a speciális kialakítása a három rögzített számos csuklós szegmensek, hogy a kapott sor szabadon lehet hajlítani két helyen (hajlítási pontok - a C és D). Meg kell tartani az aránya szegmensek: A C = B D = B 2 c d = A B >>, \; CD = AB>. Az élek a vonalak kapcsolódnak a trükköket. Amikor a nem-párhuzamos szegmensek körüli forgás a közepén a központi szelvény gócok leírni lemniszkáta Bernoulli.

lehetőség két

Ez a kiviteli alak alapja a lemniszkáta fókuszt és dupla pont - A és O, ill. Majdnem ugyanaz csuklópánt szerkezet, mint az előző kiviteli alaknál, de a csatolt egy kettős pont szegmens O C nem kapcsolódik a végén a központi B D. és annak közepén. Az arányok a többi: B C = C D = O C = A O 2. A B = A O >>, \; AB = AO>.

Az épület lemniscate segítségével metsző