Számítási hiba közvetett mérések
A kapott eredmény közvetlen mérése a valódi érték x nem mért érték, hanem egy sor
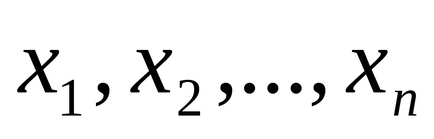
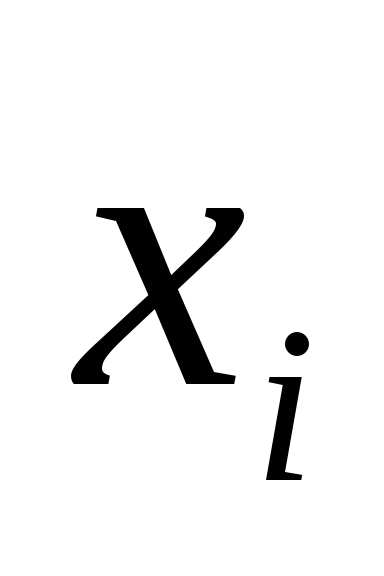
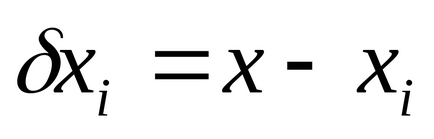
Összegezve az elmúlt egyenletet, megkapjuk
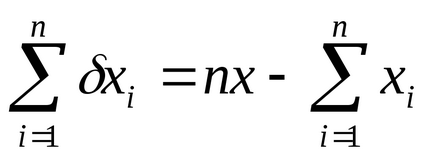
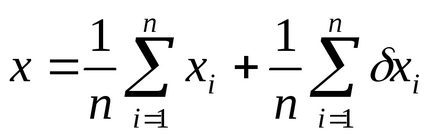
ahol
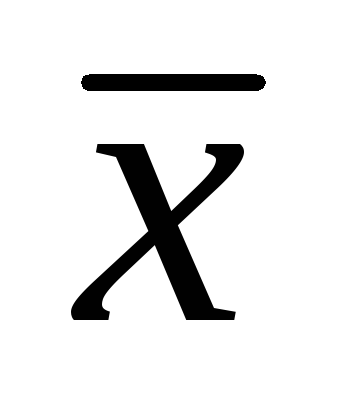
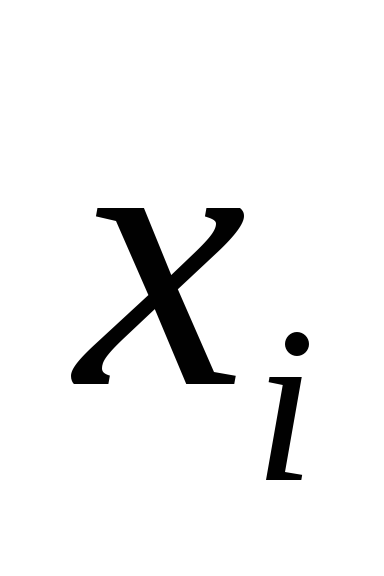
Ebből az egyszerű eredmény következik nagyon fontos következményekkel jár. Sőt, amikor
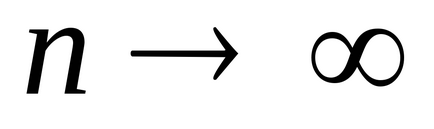
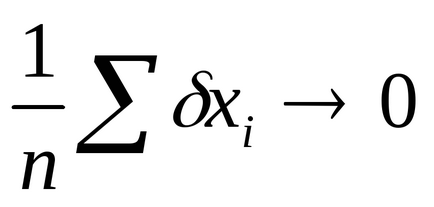
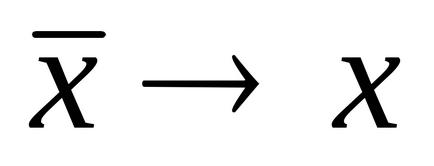
Ez azt jelenti, végtelen számú mérések
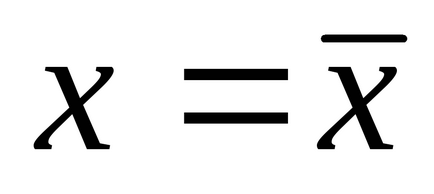
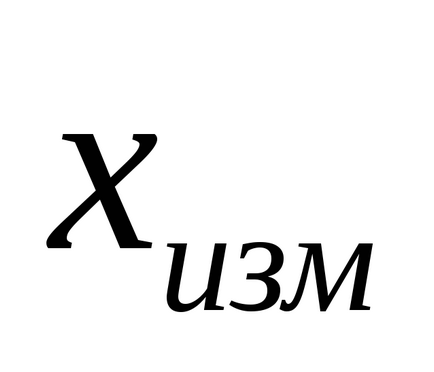
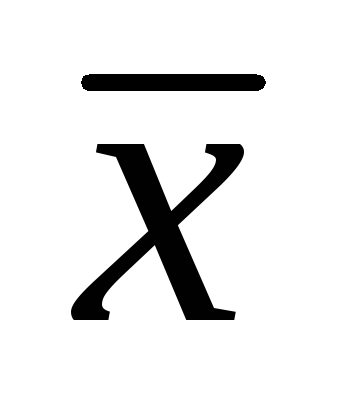
A gyakorlatban, természetesen, és n
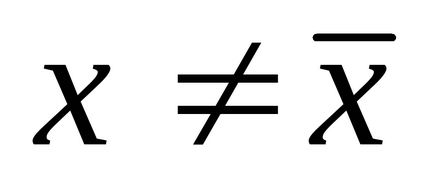
ahol fekszik a valódi értékét a mérendő. Interval (9) az említett megbízhatósági intervallumban. és az értéke
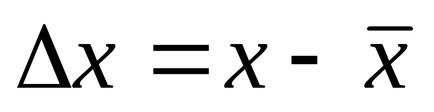
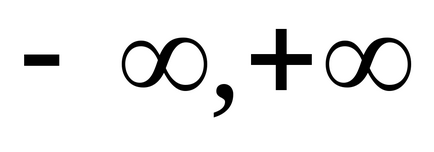
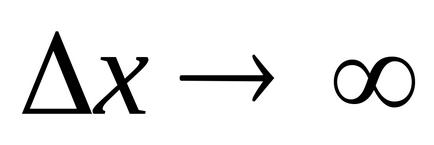
arány egyenlő a hiba Δhk négyzetes hiba *
tényező
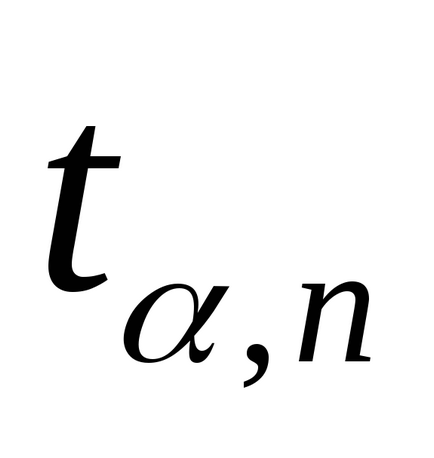
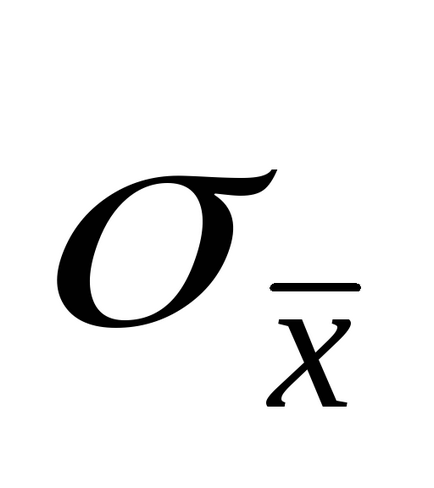
A közvetett mérések, a mért érték az f a funkcionális függőség:
ahol x. y. z - közvetlen mérés. Formula a Af állíthatók elő helyett a (2) differenciálművekhez hibákat és figyelembe összes feltételt modulo
Az összefüggés (13) ajánlatos kiszámolni a hibát Af. Műszeres hibák miatt értékek x, y, z, ... a hiba becslések társított véletlenszerű hibák közvetlen mérések a arány ajánlott:
Meg kell azonban jegyezni, hogy a képletek (13) és (14) vezet gyakorlatilag azonos eredményeket. A származékok (13) és (14) veszünk egy átlagos, azaz ha a mért értékek az érveket.
Nagyon gyakran az f függvény által képviselt hatványfüggvény függés az érvek
ahol c, n, m és p - állandó. Egyedi esetekben általános képletű (15) vannak sootnoscheniya
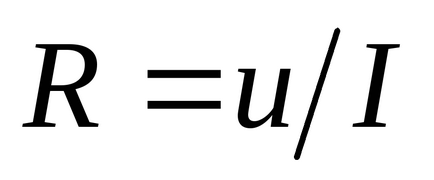
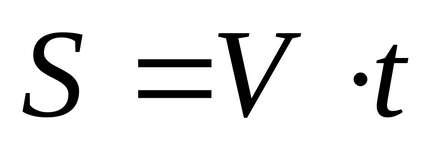
Feladat. Igazoljuk, hogy a funkciója a forma (15) általános képletű (13) és (14) formájában:
A kapcsolatok (13) és (14) az következik, hogy a számítási teljesítmény funkciók pogreschnostey jelentősen egyszerűsíteni célszerű először megtalálni a relatív hiba, amely kifejezett relatív hibája közvetlen mérés, majd találni az abszolút hiba
alatt
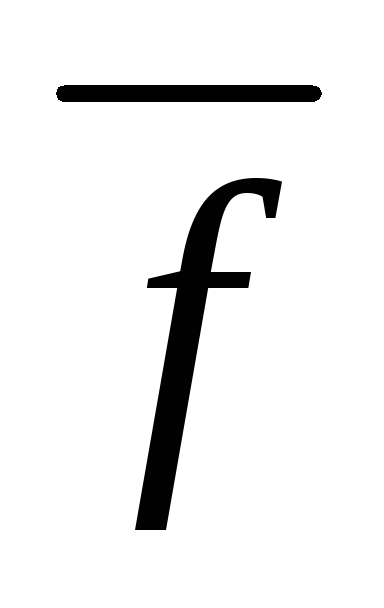
.
Algoritmus számítási hibák
- A közvetlen mérés
1. Számítsuk ki a számtani átlaga
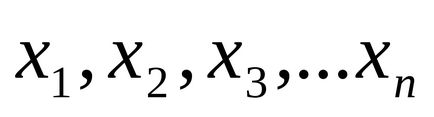
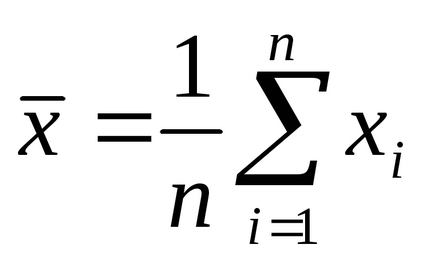
Megjegyzés: a számítás
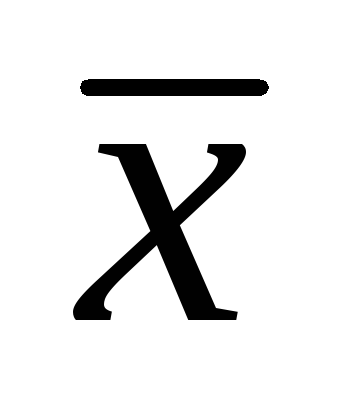
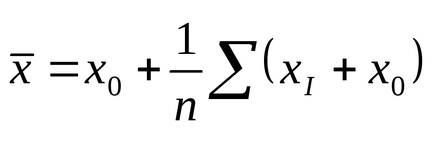
ahol
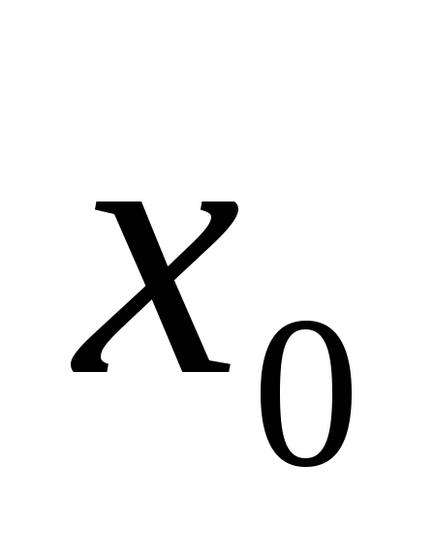
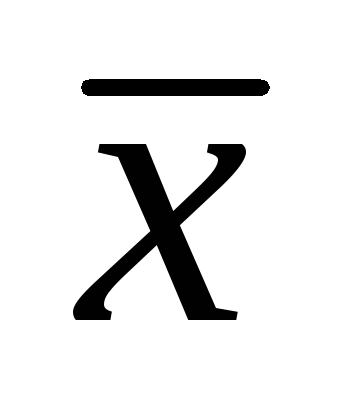
2. Keresse meg az eltérések az egyes mérések középértéke
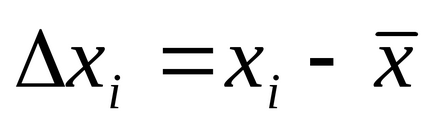
3. Távolítsuk el hibákat.
4. Kiszámítjuk az átlagos négyzetes hiba az eredménye egy méréssorozat
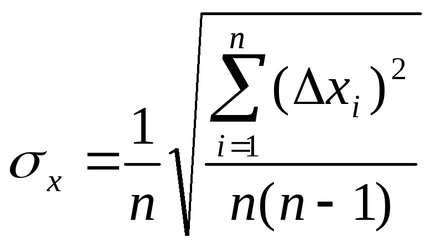
Megjegyzés. a
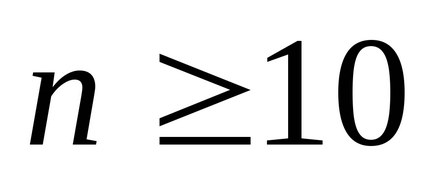
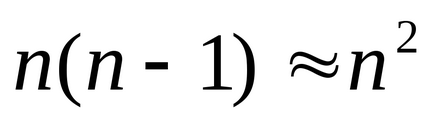
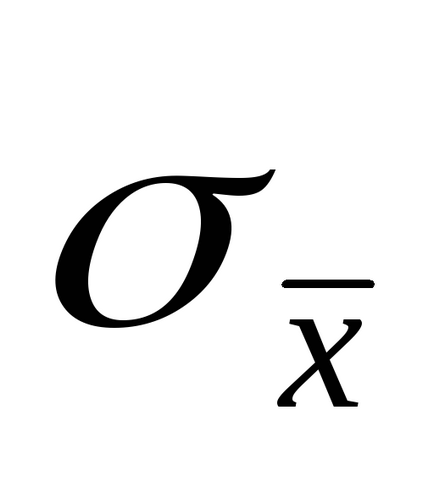
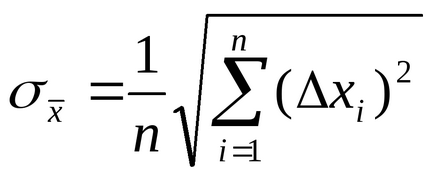
5. Amennyiben
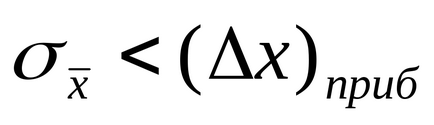
6. Egyébként adja bizalom valószínűsége

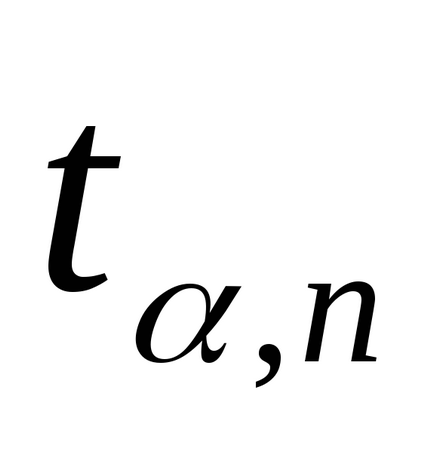
7. Becsült konfidenciahatárokat
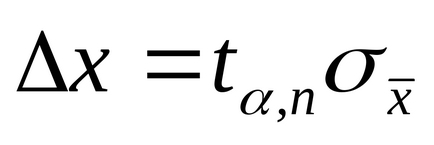
Megjegyzés: 1. Ha a készülék hibát
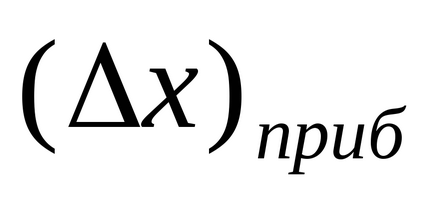
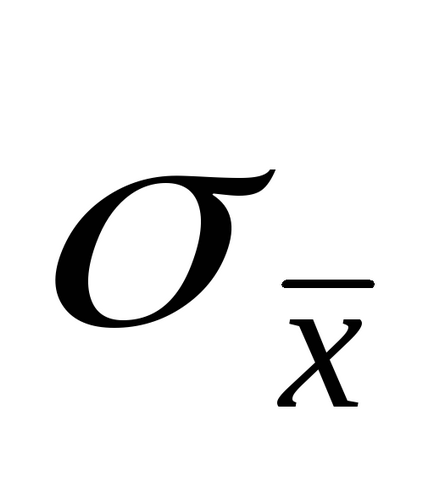
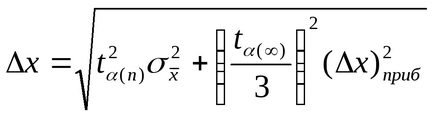
ahol
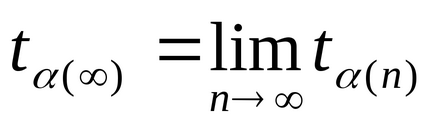
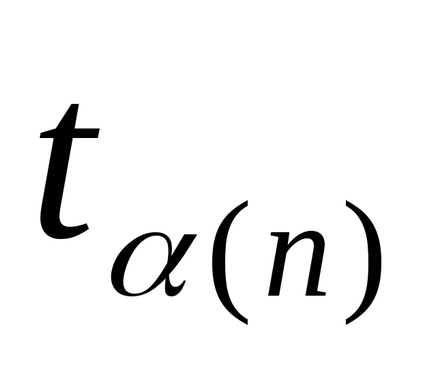
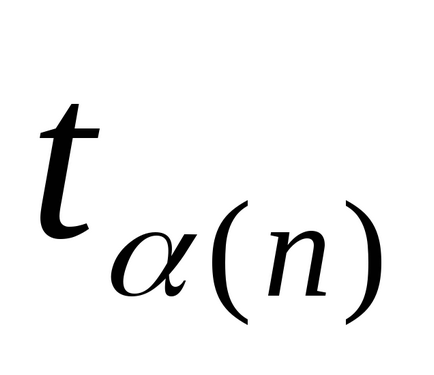
Megjegyzés 2. nagyszámú mérések
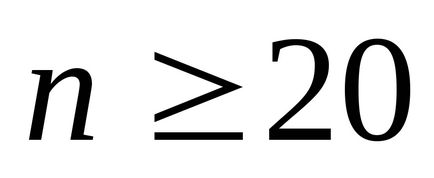
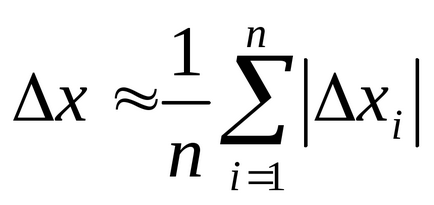
8. A mérési eredmény képviseli, mint:
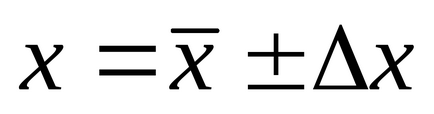
- A közvetett mérések
hiba

Áttekintés arányok kiszámításához a hiba közvetett mérési-CIÓ néhány egyszerű függvénykapcsolatok felülreprezentáltak a táblázatban.