A mozgási energia a rendszer - studopediya
A mozgási energia a rendszert nevezzük skaláris érték T egyenlő az XYZ számtani összege a kinetikus energiáját minden pont a rendszer
A mozgási energia egy jellegzetes és transzlációs hatékonysággal, a forgómozgást a rendszer, így a tétel mérhető-nenii kinetikus energia leggyakrabban használt problémák megoldásában.
Ha a rendszer több szervek, a mozgási energia nyilvánvalóan összegével egyenlő a mozgási energiák ezen szervek:
Kinetikus energia - skalár, és mindig pozitív.
Képletek kiszámításához a kinetikus energia a test különböző forgalmi esetben.
1. transzlációs mozgás. Ebben az esetben az összes pontot a test mozog az azonos sebességgel egyenlő sebességű mozgás zheniya tömegközéppont. Ez azt jelenti, hogy minden pont
Így, a kinetikus energia a test, amikor SG-transzlációs mozgás felével egyenlő a termék a testsúly patkány négyszeres sebességű tömegközéppontja. A mozgási irányának a T értéke nem függ.
2. A forgómozgás. Ha a test körül forog néhány Oz tengely (lásd. A 46. ábrán), a sebesség, annak bármely pont. ahol - a távolság a pont a forgástengely és a W - Wai szögsebessége a szervezetben. Behelyettesítve ezt az értéket, és figyelmen kívül hagyva a közös vonás, hogy a konzol, megkapjuk:
A mennyiség zárójelben, képviseli a tehetetlenségi nyomatéka a test tengelye z. Így végül megkapjuk:
t. e. kinetikus energia a test során forgási mozgás fele a termék a tehetetlenségi nyomatéka a test viszonyított forgási tengelye a négyzetével szögsebességgel. A forgásirány a T-érték független.
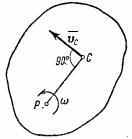
Amikor a test forgását egy rögzített pont körül úgy definiáljuk, mint a kinetikus energia (Fig.47)
ahol Ix. Iy. Iz - tehetetlenségi nyomatékok fő tengelye tehetetlenség x1. y1. Z1 egy fix pont O; . - vetülete a pillanatnyi szögsebesség ezekben tengelyek.
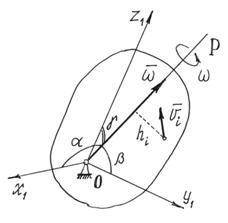
3. A síkkal párhuzamos mozgás. Ebben a mozgás-SRI sebessége minden pont a test minden egyes alkalommal eloszlás Lena, mintha a test tengelye körül forgatható síkjára merőleges a mozgás és átmegy a pillanatnyi közepén SKO növekvő P (Fig.46). ezért
ahol - a tehetetlenségi nyomaték tengelyével fenti, w- szögsebessége a test. Az érték a képlet fog változni, sósav, mivel a helyzet a központ P test mozgása-SRI folyamatosan változik. Mi cserélje állandó a tehetetlenségi nyomaték egy átmenő tengely tömegközéppontja C a test. Szerint a Huygens-tétel, ahol d = PC. Mi helyettesítheti ezt a kifejezést. Tekintettel arra, hogy a P pont - pillanatnyi sebesség center, ezért amennyiben - a tömegközéppont sebessége S. végül megszerezni:
Ezért, amikor a gép-párhuzamos mozgás a kinetikus energia a test-LIC energiával egyenlő a transzlációs mozgás a tömegközéppont sebessége réteg-zhennoy skineticheskoy energiája forgómozgás körül a tömegközéppont.
4) A legáltalánosabb esetben a mozgás a kinetikus energia a rendszer segít kiszámítani a tétel a Koenig.
Nézzük meg a mozgás a rendszer, mint a kettő összege (Fig.48). Hordozható - transzlációs mozgást együtt tömegközéppontja C, a relatív - relatív transzlációs mozgása együtt mozgó tömegközéppontja a tengelyek X1, Y1, Z1. Ezután a sebességet a pontokat. De ábrás mozgás - előre. Ezért hordozható aránya az összes pontok egyenlő. Ennélfogva a mozgási energia lesz
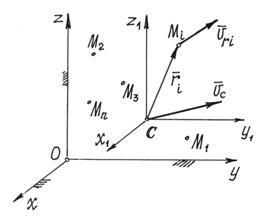
Definíció szerint, a tömegközéppontja a sugár vektor a mobil rendszerben (a súlypont a származási), így. Az idő származéka Ez az összeg is egyenlő nullával:
Ezért végül a kinetikus energia a rendszer
A mozgási energia az anyagi rendszer az összege kinetikus energiát előre mozgás a tömegközéppont és kinetikus energia mozgása alatt képest koordinátatengelyeken, transzlációs együtt mozgó tömeg közepén.
Általánosságban, a test mozgása, amely lehet tekinteni, mint a kettő összege (hordozható - transzlációs együtt tömegközépponti és a relatív - körüli forgatás C pont) Koenig tétel (1) megkapjuk
ahol Ix. Iy. Iz - a legfőbb központi tengelye tehetetlenség.