Vizsgálatok - egyszerű véletlen szám generátor
Ebben a cikkben megmutatom, hogyan kell létrehozni véletlen számok segítségével négy különböző algoritmusok: Lehmer algoritmus (Lehmer) lineáris kongruencia algoritmus (lineáris kongruencia algoritmus), az algoritmus Wichmann-Hill (Wichmann-Hill), és az algoritmus Fibonacci Delay (késleltetett Fibonacci algoritmus) .
De miért terheld magad létre saját véletlenszám-generátor (véletlenszám-generátor, RNG), amikor a Microsoft .NET Framework már egy hatékony és egyszerűen használható osztály Random? Két forgatókönyv, ahol szükség lehet, hogy saját RNG. Először is, a különböző programozási nyelvek épülnek a különböző algoritmusok véletlen szám generálás, ami azt jelenti, hogy ha írunk kódot kerül át több nyelven, akkor létrehozhatunk saját RNG annak végrehajtására minden nyelven, amit akar. Másodszor, bizonyos nyelvek, például az R, csak globális RNG, ezért ha azt szeretnénk, hogy hozzon létre több generátorok, meg kell írni a RNG.
Egy jó módja annak, hogy egy ötlet, hol fogok ebben a cikkben - nézd meg a példaprogramot látható. 1. Bemutató program kezdődik létrehozásával egy nagyon egyszerű RNGYU segítségével Lehmer algoritmus. Majd az RNG 1000 generál véletlen egészek 0 és 9 között is beleértve. A színfalak mögött rögzített számlálók az egyes generált egészek, amelyeket aztán megjelenik a képernyőn. Ez a folyamat ismétlődik egy lineáris kongruencia algoritmus Wichmann-Hill algoritmus és Fibonacci algoritmus késések.
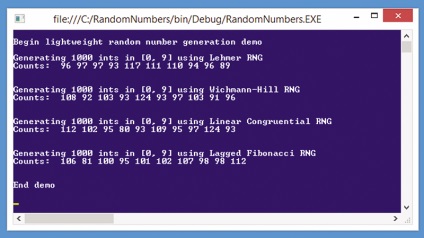
Ábra. 1. bemutatása egyszerűsített véletlen számok generálása
Ez a cikk feltételezi, hogy tudja, hogyan kell programozni legalább az átlagos szintet, de nem tud semmit a véletlen számok generálása. A demonstrációs program írt C #, de az egyik fő felhasználási saját véletlenszám generálás - írásban hordozható kódot, a program úgy van kialakítva, hogy lehet könnyen lefordítani más nyelvekre.
Lehmer algoritmus
A legegyszerűbb módszer alkalmas a véletlen szám generálás - Lehmer algoritmus. (Az egyszerűség kedvéért használjuk a „véletlen szám generátor” helyett a pontosabb kifejezést „véletlen szám generációs”.) Kifejezve szimbolikusan, Lemaire algoritmus a következőképpen:
A szavak, úgy hangzik, mint ez: „egy új véletlen számot a régi véletlen számot megszorozzuk a legállandóbb, majd az eredmény a művelet modulo állandók m». Tegyük fel például, hogy egy bizonyos ponton az aktuális véletlen szám egyenlő a 104, a = 3 és m = 100. Ekkor egy új véletlen számot egyenlő 3 * 104 mod 100 = 312 mod 100 = 12. Úgy tűnik, hogy egyszerű, de végrehajtása során ezt az algoritmust, egy csomó okos részleteket.
Ahhoz, hogy hozzon létre egy demonstrációs program, elindítottam a Visual Studio, úgy döntött, C # Console Application sablon és elemzi RandomNumbers projekt. Ebben a programban, nincs jelentős mértékben függ a .NET Framework, így illeszkedik bármely változata Visual Studio.
Ábra. 2. A végrehajtás az algoritmus Lehmer
Egy végrehajtási problémát, hogy ne aritmetikai túlcsordulás. Lehmer féle algoritmus egy ügyes trükk algebrai. Az érték q az eredménye m / a (osztás), és r értéke egyenlő m% egy (m mod a).
Inicializáláskor RNG Lehmer primer (embrionális) érték bármely egész szám lehet a tartományban [1, int.MaxValue - 1]. Sok a RNG nem-érv kivitelező, hogy megkapja a rendszer dátumát és idejét, átalakítja egy egész, és ezt használjuk a kezdeti érték.
Lehmer RNG hívják a Fő módszer demonstrációs program:
Minden hívás Következő metódus visszaad egy értéket a tartomány [0,0, 1,0) - nagyobb vagy egyenlő, mint 0,0 és szigorúan kisebb, mint 1,0. Sablon (int) (hi - lo) * Következő + lo) tér vissza közötti egész szám [lo, hi-1].
Lehmer algoritmus nagyon hatékony, és egyszerű forgatókönyv, szoktam választani, hogy pontosan azt. De észre, hogy sem a bemutatott algoritmus ebben a tanulmányban nem rendelkezik a megbízhatósági szint kriptográfiai és hogy kell használni, csak azokban az esetekben, amelyek nem igényelnek statikus szigor (statisztikai szigor).
Algoritmus Wichmann-Hill
Ez az algoritmus kelt 1982 évben. Wichmann Hill ötlet az, hogy létrehoz három előzetes eredményeit, és egyesíti őket egy végeredményt. A kód, amely megvalósítja az algoritmus Wichmann-Hill, ábrán látható. 3. A demo-kód alapján a cikket BA Wichman (B. A. Wichmann) és A. J. Hill (I. D. Hill) «algoritmus 183: Hatékony és hordozható pszeudo-véletlenszám generátor».
Ábra. 3. A végrehajtás az algoritmus Wichmann-Hill
Mivel az algoritmus Wichmann Hill használ három különböző előállító egyenlet van szükség, mert a három eredeti értékeket. Ebben az algoritmusban a három m-értékek 30269, 30307 és 30323, ezért van szükség a három kezdeti értékek a tartomány [1, 30000]. Írhatsz egy kivitelező, hogy úgy ez a három érték, de akkor is kap néhány bosszantó szoftver interfész. A bemutató használható egyetlen paraméter kezdeti értékét előállító három munkanapon embrió.
Hívjon RNG Wichmann-Hill hordozza ugyanazt a mintát követi, mint a többi bemutató RNG:
Wichmann-Hill algoritmus csak kicsit nehezebb megvalósítani, mint az algoritmus Lehmer. Az előnye, hogy a korábbi, mint a második, hogy az algoritmus Wichmann Hill generál egy hosszabb sorozatot (több mint 6 000 000 000 000 érték), mielőtt elkezdik ismételni.
Lineáris egybevágó algoritmus
Úgy tűnik, és Lehmer algoritmus, és az algoritmus Wichmann-Hill is tekinthető különleges esetekben az úgynevezett lineáris kongruencia algoritmus (lineáris kongruencia, LC). Kifejezve, mint egy egyenlet, LC a következő:
Ez pontosan megfelel az algoritmus Lehmer hozzá több állandó c. Engedélyezése c ad Universal LC-algoritmus valamivel jobb statisztikai tulajdonságokkal rendelkezik, mint az algoritmus Lehmer. Bemutató végrehajtás LC-algoritmus ábrán látható. 4. A kód alapjául szabványos POSIX (Portable Operating System Interface).
Ábra. 4. Végrehajtás egy lineáris kongruencia algoritmus
LC-algoritmus számos kicsit műveleteket. Itt az ötlet, hogy az alap matematikai típusok nem működik egész típusú (32 bit), és egy hosszú egész (64 bit). Végén 32 A bitek (a 16. a 47. befogadó) extraháltuk, alakítjuk egy egész szám. Ez a megközelítés jobb eredményt ad, mint egy 32-bites fiatalabb vagy idősebb, de amiatt, hogy néhány szövődménye kódolás.
A bemutató egy véletlenszám-generátor úgynevezett LC:
Bemutató előző kód használja a véletlenszám X (i-7) és X (i-10), hogy létrehozzuk a következő véletlen szám. A szakirodalom ebben a témában értékek (7, 10) általánosan említett (j, k). Vannak más párt (j, k), amelyeket fel lehet használni a Fibonacci algoritmus késések. Számos ajánlott értékeket egy jól ismert könyve «Art of Computer Programming» (Addison-Wesley, 1968) - (24.55) (38.89) (37,100) (30,127) (83,258) (107,378) .
Inicializálja (j, k) az RNG Fibonacci késések, először meg kell töltenie egy listát a k értékeket. Ezt meg lehet tenni számos módon. Azonban, a kisebb a kezdeti értékek k kell páratlan. A demonstrációs használt nyers módszer a másolás értékek vetőmag értéket az összes kiindulási értékeit K, majd ezt követően eltávolítjuk az első 1000-generált értékek. Ha a paraméter értéke vetőmag páros, akkor az első k értéke van beállítva egyenlő 11 (tetszőleges páratlan szám).
Annak megakadályozása érdekében túlcsordulás, Következő típusú módszer hosszú számítások és matematikai tulajdonsága: (a + b) mod n = [(a mod n) + (b mod n)] mod n.
következtetés
Hálámat felülvizsgálatára Microsoft lesz a szakértő Chris Lee (Chris Lee) és Oliniku Kirk (Kirk Olynyk).