Vektor terméket adott koordináták a kevert termék - a problémák megoldását,
Vektor terméket adott koordináták kevert termék

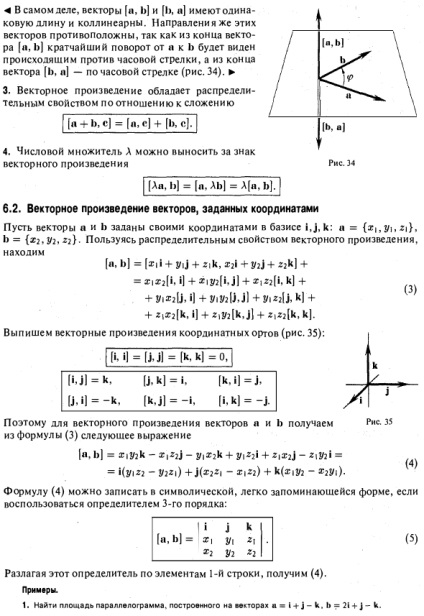




Definíció. A vektor termék egy vektort és egy B vektor a vektorba, Jele [”, b] (vagy L x L) úgy, hogy 1) a hossza a vektor [a, b] jelentése (p, ahol - közötti szög a és b vektorok ( ábra31); 2) a vektor [a, b) merőleges az a és b vektorok, azaz. síkjára merőlegesen e vektorok; 3) a vektor [a, b] irányul úgy, hogy a végén a legrövidebb vektor rotációs tól b látható előforduló az óramutató járásával ellentétes (ábra. 32). Ábra. 32 ábra31 Más szóval, a vektorok a, b, és [a, b) alkotnak jobbkezes vektorok, azaz a elhelyezni a hüvelykujj, mutatóujj és a középső ujj a jobb kezét. Ha a vektorok a és b egy egyenesbe esik, akkor feltételezzük, hogy a [a, b] = 0. A meghatározás szerint a hossza a vektor termék számszerűen egyenlő a terület Sa a paralelogramma (33. ábra) felépítve a szorzatát a és b vektorok mindkét oldalán: 6.1 . Tulajdonságok A vektor termék 1. A kereszt termék egyenlő a nulla vektor tolkotogda ha és amikor legalább az egyik a megszorzott vektorok nulla, vagy ha ezek a vektorok egy egyenesen vannak (ha a vektorok a és b egy egyenesbe esik, a köztük lévő szög 0 vagy 7d). Ez könnyen kap az a tény, hogy ha feltételezzük, nulla vektor kollinsarnym bármilyen vektor, akkor a feltétele kollinearitása a és b vektorok fejezhető 2. A vektor termék anticommutative, t. E. mindig. Valóban, a vektorok (a, b), és a [Li, «] azonos hosszúságú, és egy egyenesbe esik. Azonos irányban ezek a vektorok a szemben, mert a végén a vektor [a, b] a legrövidebb forgás tól b-ig lesz látható előforduló az óramutató járásával ellentétes, és a végén a vektor [b, a] - az óramutató járásával megegyező (ábra. 34). 3. A vektor termék forgalmazási tulajdonság tekintetében a kiegészítéssel 4. A numerikus tényezővel lehet venni, mint egy jel a vektor termék 6.2. Vector termék megadott koordináták Legyen az a és b vektorok által adott annak koordinátáit alapján. Az elosztó tulajdonában vektor terméket találunk a vektor termék vektorok a megadott koordináták. A kevert termék. Írjunk a vektor termék a koordináta egység vektorok (35. ábra) Ezért, a vektor termék a és b nyert (3) képlet, a következő kifejezés képletű (4) felírható szimbolikus, könnyen megjegyezhető módon, ha használjuk a meghatározója a harmadik rend: bővítése meghatározó elemei által az 1. sor, azt kapjuk, (4). Példák. 1. Keresse meg a területet a paralelogramma épített a vektorok keresési terület tehát találunk, ahol = 2. Keresse meg a háromszög területe (ábra. 36). Egyértelmű, hogy a háromszög b'd terület felével egyenlő az S felület a paralelogramma Körülbelül AU B. számítása a kereszt az (a, b | vektorok a = OA és b = Ob, megkapjuk Megjegyzés: A szorzat nem asszociatív, hogy az egyenlőség (. (a, b), c) = [a, | b, c)) az általános esetben nem igaz. Például, ha a = SS j lett § 7. A vegyes termék vektorok Tegyük fel, hogy három vektor a, b és c. Szorozzuk meg a vektorok a és 1> vsktorno. Az eredmény a vektor [a, 1>]. Szorozza meg a vektort (a b), c). A számát ([a, b], f) az úgynevezett vegyes termék a és b vektorok. c és jelöljük (a, 1), e). 7.1. A geometriai jelentése a kevert termék Postpone vektorok a, b és c otobshey O pont (ábra. 37). Ha mind a négy pont O, A, B, C egy síkban fekszik (a vektorok a, b és c nevezzük ebben az esetben egy síkban), a kevert termék ([a, b], s) = 0. Ez abból a tényből következik, hogy a vektor [a, b | merőleges a síkra, amelyben fekszenek a vektorokat a és 1”, és így a vektort. / Ha az O pont, A, B és C nem fekszenek egy SVOCs-csont (a vektorok a, b és egy nem-koplanáris), épít a szélek OA, OB és OC egy doboz (ábra. 38 a). A definíció szerint a kereszt termék van (a, b) = Tehát, ahonnan Tehát - paralelogramma területen OADB, és - egy egységet vektor merőleges a a és b vektorok, oly módon, hogy a hármas a, b, c - a megfelelő, azaz vektorok a, b és c vannak elrendezve, illetve, ahogy a hüvelykujj, mutatóujj és a középső ujj a jobb kéz (ábra. 38 b). Megszorozzuk mindkét oldalán az egyenlet jobb vektor által megszerezni, hogy a vektor termék megadott koordináták. A kevert termék. A száma CSG azonos h magassága van kialakítva parallelepipedon, együttesen a „+” jel, amikor a szög vektorok között S és az akut (a hármas a, b, c - jobbra), és a „-” jel, amikor a szög - tompaszöget (tripla is, b, c - bal), úgy, hogy ez a módja, a kevert termék vektorok a, b és c jelentése megegyezik a V térfogata a paralelepipedon épített ezek a vektorok, mint a bordák, ha a hármas a, b, c - a megfelelő, és a -V, és ha a hármas a, b, c - balra. Ennek alapján a geometriai jelentését a vegyes termék, arra lehet következtetni, hogy megszorozzuk tf vektorok a, b és c bármilyen más sorrendben, akkor mindig kap 7 vagy -K. Bejelentkezés proiz- ábra. 38 magatartás függ csak azért, mert néhány három alkotják a megszorzott vektorok - jobbra vagy balra. Ha a vektorok a, b, c alkotnak jobbkezes, akkor a jogok is hármas b, c, a és c, a, b. Ugyanakkor mindhárom háromágyas b, a, c; a, c, b, és c, b, a - balra. Így, (a, b, c) = (b, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (a, b is). Esheraz hangsúlyozzák, hogy a vegyes termék vektorok egyenlő nulyutogdai csak akkor, ha a megszorzott vektorok a, b, és c egy síkban vannak: 7.2. A vegyes termék vektorok koordinátákkal Legyen a, b, és c kapnak a koordinátái által a bázis i, j, k: a = b = z2>, c =. Keressük azt a kifejezést, hogy a vegyes termék (a, b, c). Van vegyes termék vektorok alapján zadannyhsvoimi koordináták i, j, k, egyenlő a meghatározója a harmadik rend, amelyben a húzott, illetve a koordinátáit egy első, második és harmadik vektorok a szorzandó. A szükséges és elégséges feltétele coplanarity a vektorok \, Z |>, b =, c = lehet írott formában U | Z, AZ2 y2 = 0 -2. Példa Uz. Ellenőrizze, hogy a vektorok „egy síkban = b = c =. A megfontolt vektorok lesz egy síkban vagy nem egy síkba eső függően, egyenlő lesz nulla vagy nem meghatározó a bővülő elemei az első sorban, kapjuk a D = 7- 6- 4- 15 + 6-3 = 0 ^ - vektorok N, b, c egy síkban vannak. 7.3. Double Double kereszt terméket vektor termék [a, [b, c]] az a vektor merőleges a vektorok a és [b, c]. Ezért síkjában vektorok b és c, és lehet bontani ezek a vektorok. Meg tudjuk mutatni, hogy van a képlet [a, [> s]!] = L (a, e) - a (a, b). Gyakorlatok 1. A három vektort AB = c, F? = O = b és a CA az egy háromszög oldalai. Kifejezve az a, b és c vektorok, a medián egybeesik AM, DN, CP háromszög. 2. Milyen feltételeket kell vonni vektorok p és q, a vektor p + q megosztott a köztük lévő szög fele? Azt feltételezik, hogy mind a három vektor kapcsolódnak az általános tetején. 3. Számítsuk ki a átló hosszát a paralelogramma épített a vektorok a = 5p + 2q és b = p - 3q, ha tudjuk, hogy | p | = 2V / 2, | q | 3 = H- (p7ci) = f. 4. jelölő a és b oldalán a rombusz áll, amely közös vertex, bizonyítja, hogy az átlós a rombusz kölcsönösen merőlegesek. 5. Számítsuk ki a skalár szorzata vektorok egy = 4i + 7j + 3K és b = 31 - 5j + k. 6. Keresse az egység vektort a0, párhuzamos vektorok a =. 7. Find a nyúlvány a vektor a = l + j- Kha vektor b = 21 - j - 3K. 8. Find a koszinusza közötti szög a vektorok IS «f, ha A (-4,0,4), B (-1,6,7), C (1,10.9). 9. találja a készüléket vektor p °, mind merőleges és a vektor a = Ox. 10. Számítsuk ki a szinusz közötti szög az átlók parallelofamma által alkotott vektorok egy = 2i + J-K, b = I-3j + k mindkét oldalon. Számítsuk ki a h magassága a paralelepipedon által alkotott vektorok egy = 31 + 2j - 5k, b = i- j + 4knc = i-3j + k, ha aljáról vett a paralelogramma által alkotott vektorok a és I). válaszok