Változás száma, tartomány és hisztogram
A sorok allokációs sorozatszáma, jellemző szerkezete az aggregált néhány területen. Számos eloszlás eredményeként kapott szerkezeti csoportok. Számos eloszlása által alkotott változók (variációs tartomány) lehetnek diszkrét (attribútum vesz egy korlátozott számú lehetséges értékek, például 2,3,4,5), illetve szakaszos (jellemző érték által kifejezett valós számok, vagy a számos lehetséges attribútum értékek elég nagy).
Jellemzői a sorozat:
xi - kiviteli alak (esetleges külön numerikus jellemző érték)
ni - gyakorisága (több különálló csoportok);
n - az összes elem együtt;
qi - relatív gyakorisága (az arány az egyes csoportok teljes egészében).
Variációs sorozat készül egy asztal, ahol az első oszlopban változatok (intervallum) jellemző értékeket, és az alábbi - a frekvencia és a relatív gyakorisága.
Számos elosztó egészének struktúrájára jellemző az aggregátum egy adott tulajdonság. Azonban lehet használni, és a halmozott sorozat, azaz a sorok kumulatív gyakoriság (relatív frekvencia).
Összesített frekvencia (relatív gyakoriság) - az első számú (frakciója) halmaz elemeit, amelyben a jellemző értékek nem haladják meg ezt.
F (x) - kumulatív frekvencia egy adott x értékét,
G (x) - kumulált relatív gyakorisága egy adott x érték.
Ezek a jellemzők a következő tulajdonságokkal rendelkezik:
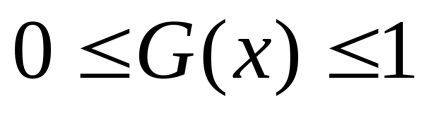
Tekintsük az intervallum száma i. [xi
Összesített gyakorisága végén az i-edik intervallumot képlet határozza meg
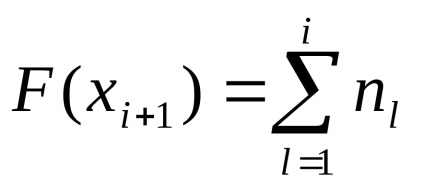
Változás szám is képviselteti magát egy grafikont.
A kép egy különálló sorozat sokszög. Amikor épület ez az abszcisszán kiviteli alakoknál a (XI), és az ordináta - relatív gyakoriság vagy frekvencia - fi. Ezután a pont a koordinátái (xi; fi) egymás után kötve vonalszakaszok.
A kép a idõközsorozat a hisztogram. Az építkezés az abszcisszán az intervallumok a sorozat. Fent abszcisszán épített téglalap, amelynek alapja az az időköz és magassága - a frekvencia vagy a relatív gyakoriság.
A fényképek halmozott száma frekvenciák halmoz. Kumulatív frekvencia függvényében ábrázoljuk az y-tengelyen intervallumok határain, és ezek egymáshoz vonalszakaszok.
1. példa Az eloszlás a lakások a lakosság száma látható a táblázatban otthon. Construct sokszög, és halmoz.
Az élő emberek száma a lakásban
Találunk a medián. Ebben az esetben,
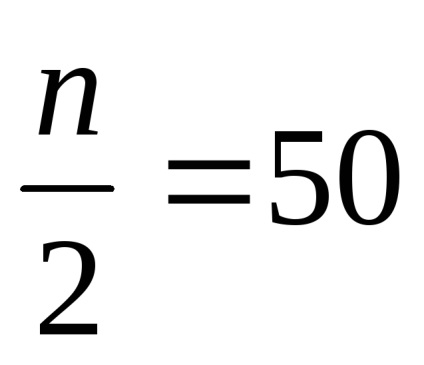
Meg fogjuk találni a divat ezekből az adatokból. Divat ugyanabban a tartományban, mint a maximális frekvencia (25) vannak ebben az intervallumban.
.
.
.
szabvány eltérés
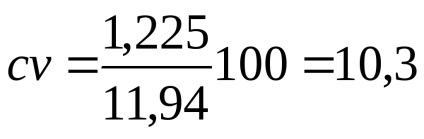
Alapján szerkezeti csoportok második jelzés kapott feladatot 1, és halmoz hisztogram.
Számított a csoportosított adatok:
variancia és a szórást;
Abszolút és relatív statisztikák. Kiszámítása átlagérték relatív mutatók.
Az abszolút számok a statisztikában, hogy megértsék alapszintű statisztikai felmérések (termelési volumen emberek száma, és így tovább. D.). Lehetnek nyomaték (az adott időpontban), és időközben (egy bizonyos ideig). Bármely abszolút érték (index) olyan belső mérőegység (db, kg, m, és a hasonlók. D.). Gyakran a költség paraméterek (rubelben) használunk az abszolút mutatókat.
Az relatív mutató statisztika, hogy megértsék a számok, jellemző aránya két abszolút mutatók (egy főre jutó GDP, a munka termelékenysége, a termelési költségek, és így tovább. D.).
Különböztesse relatív értékek szerkezete, koordináció, dinamika, intenzitása és összehasonlítása.
Relatív értékek jelentik a százalékos a szerkezet minden egyes csoport a teljes populációban. Nyerik számát elosztjuk az egyes csoportok által a méret a teljes népesség.
Relatív kapott értékek koordináta arányként részei között egy sor. Például, lehet, hogy az arány a férfiak és nők.
A mértékének arányban az összehasonlítás összehasonlításával kapott a két szám az azonos nevű, tartozó különböző aggregátumok. Például, ha összehasonlítjuk a tárgyi eszközök értéke két különböző régiókban.
A relatív nagysága az intenzitás összehasonlításával kapott jelei egy készlet ellentétes töltéseket. Például, a termékenységi ráta az aránya a születések száma, hogy a lakosok száma, és a termelési költségek az aránya a teljes költségek tömegtermelést.
Határozni az átlagos értékek relatív értékeit különböző képletekkel használt súlyozott átlagok alapján a gazdasági mutatók jelentését. A statisztika által használt különböző átlagokat.
Leggyakrabban a következő átlagos értékeket kell alkalmazni:
Mindezek a átlagértékeket lehet kiszámítani a teljesítmény átlagos általános képletű
Ha az adatokat csoportosítva, majd
Az utolsó két képlet teszik lehetővé olyan különféle közepes különböző m értékek (lásd. Táblázat).
A számtani középértéket, harmonikus átlag, a geometriai átlag és átlagos négyzetes számított azonos bemeneti adatok eltérnek egymástól. Mindig van a következő összefüggést:
Íme néhány példa a használatát súlyozott átlagok függőségek.
1. példa ki az átlagos teljesítmény együtthatót a terv a vállalkozások ág.
Let - i- edik terv a vállalkozás;
- relatív mutató kiviteli terv (a frakciók);
N - száma az iparban.
Ezután a tényleges termelés volumene lesz
A tervezett termelési volumen az ipar
A medián a terv az ágazat
Ez az index a súlyozott átlag számtani metrikák megfelelő súlyozással termelési terv -.
2. példa ki az átlagos jármű sebességét, ha ő megtett távolságot S1 sebességgel v1. majd a távolság S2 sebességgel v2. Ahhoz, hogy megtalálja az átlagsebesség kell osztani a teljes távolságot S1 + S2 teljes időt töltött ezen a módon. A teljes menetidő egyenlő lesz
Így az átlagos sebesség lesz
Általában, jelenlétében N szakaszok különböző sebességgel
Ez könnyen belátható, hogy az átlagos sebesség a súlyozott átlaga harmonikus sebességek az egyes szakaszok súlyokkal megegyezik a hossza a pályaszakaszok.