Tulajdonságok logaritmus (logaritmus fok)

A tulajdonságok nyert logaritmusát annak meghatározása. Egy jól ismert tény, hogy a logaritmusa b a bázis és úgy definiáljuk, mint egy exponens. szeretné emelni a száma a, b, hogy a szám.

Kapjuk szövegéből nyilvánvaló egyenlőség LOGA 1 = 0, mert a 0 = 1, és loga a = 1, mivel a 1 = a.

Tekintsük a helyzetet, amikor a bázis a logaritmus az érv vagy a szükséges mértékben. Ekkor a mutató ilyen mértékű lehet venni jeleként logaritmusát a következő szabályokat:

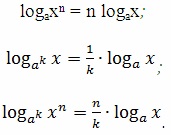
Természetesen mindezek képletek értelme megfelel a jelenlegi területe a logaritmus értékek. a> 0, a ≠ 1, x> 0. Továbbá, mindegyiket lehet használni nem csak balról jobbra, hanem éppen ellenkezőleg, ezért hagyjuk mozogni a számok felé logaritmusát önmagában logaritmus. Tulajdonképpen ez gyakran történik.

A logaritmusa fokának pozitív számok a termék a fokának indexe annak alapja a logaritmus:

Vagy tegye könnyebbé, ebben az esetben, a kitevő kivenni, mint tényező. eredményeképpen időigényes művelet hatványozási változás egy elemi szorzás művelet.

2) log7 49 6 = 6log7 49 = 6 · 2.

A negatív értékek x általános képletű értelmetlenné válik. Így, tilos, hogy írjon log2 (- 4) 2 = 2log2 (- 4), mint a kifejezés log2 (- 4) nincs definiálva. Fontos megjegyezni ugyanakkor, hogy ez a kifejezés bal oldalán a képlet, akkor is van értelme: