tulajdonságok gyökerek
A tulajdonságait négyzetgyökvonás.
- ;
- Ha egy ≥ 0 és b> 0;
- Ha egy ≥ 0, és n - egy egész szám;
- Ha egy ≥ 0 és n - természetes szám.
- Megjegyzés (5) 2 = 25, de.
- A gyökér nem lehet egyenlő a számát nem pozitív.
- - lehetetlen kiszámítani a négyzetgyök negatív szám nem létezik.
- Ha, akkor b 2 = a. amikor egy ≥ 0 és b ≥ 0. egyik legfontosabb tulajdonságai a gyökerek.
- Fontos megérteni, hogy a négyzetgyök - újabb belépő szintű ½:
- gyökér értéke nem változik, ha a kamatemelés, hogy n-szer, és ugyanabban az időben, hogy egy négyzetgyök értéke erejét n:
- gyökér érték nem változik, ha a kitevőt csökken n-szer, és ugyanabban az időben kivonat a gyökér a n-ed-fokú a négyzetgyök értékek:
- A gyökér a hányados egyenlő a hányadosa négyzetgyöke az osztalék az osztó gyökere (gyökerek mutatók azonosnak kell lennie):
- Ahhoz, hogy épít gyökér a mértéke elég építeni ezen a szinten a négyzetgyök értéke:
Fordítva, hogy távolítsa el a gyökér a mértéke, hogy egyenesen elég ekkora gyökér a talajszint:
- A gyökér a termék több tényező egyenlő a termék a gyökerek az azonos fokú ezen tényezők (is fontos tulajdonsága a gyökerek):
Ezzel szemben, a termék a gyökerek az azonos mértékben megegyezik az azonos gyökér a termék az értékek a gyökök:
A négyzetgyök egy elemi függvény.
Négyzetgyök - ez egy elemi függvényt és egy speciális esete a hálózati funkció. Aritmetikai négyzetgyök sima mikor és nulla, folyamatosan a jobb oldalon, de nem differenciált (megkülönböztetett svoytvo gyökerek).
Ennek függvényében a komplex változó gyökér - egy két értékű függvény, amely felsorolja konvergál a nullához.
Az ingatlan függvényében a gyökér.
A [0; + ∞) lehet szállítani, minden számot x szerinti Singular gyökere fokú N-x bármelyik értéke n.
Ez azt jelenti, hogy a forgatáson [0; + ∞) beszélhetünk a gyökér funkció:
Most határozza meg a tulajdonságait a gyökér funkció és a kivitelezést a grafikonon.
A főbb jellemzői a gyökér függvényében:
A [0; + ∞) - a domain.
Mivel a nem-negatív szám a gyökere n-fokú, nem-negatív szám, akkor a [0; + ∞) a domain függvény értékei.
Mivel a szimmetrikus halmaz nem a domain a funkció, így a funkció nem páratlan és nem is.
A művelet kitermelése a gyökér adjuk inverz művelet emelése megfelelő mértékben.
Tehát azt lehet mondani, hogy:
Most megadhatók a gyökér funkciót.
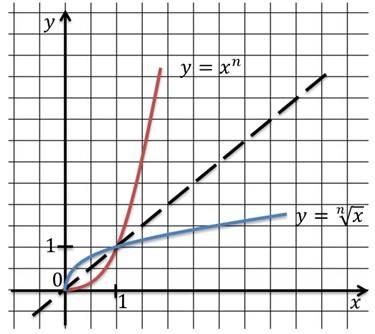
A grafikon, tudjuk írni a maradék tulajdonságait a funkciót.
A [0; + ∞) funkció növeli.
Top funkció nem korlátozott, de ez korlátozott alulról, például egy egyenes vonalat, amely = -0.5.
Az egész tartomány a függvény konvex, felfelé irányuló.
Mi jellemző a legalacsonyabb érték 0 lesz, és a legnagyobb érték van.
Ha az egyes pontok bizonyos intervallum függvény differenciálható, az azt jelenti, hogy egy adott időszakban folyamatos.
Bármely pontján a [0; + ∞) létezik, ez a származék, az egyetlen kivételt az a pont 0.
Mivel bármely pontján a (0; + ∞) függvény egy származéka, az azt jelenti, a (0; + ∞) függvény differenciálható.