Tételek a differenciálható függvények
Összehasonlítva ezeket egyenletek azt mutatják, hogy a származék egy adott ponton az útvonalon vektor egy maximális értéke, amikor a vektor iránya egybeesik az irányt a gradiens. Ez a legmagasabb értékét a derivált egyenlő a modulusa a gradiens ezen a ponton. Ezért, a gradiens vektor irányát jelzi legnagyobb növekedést a függvény ezen a ponton, és annak egysége - maximális növekedés üteme.
Példa 16,8. Dana funkciót. Keresse meg a derivatív pontnál
M (1, 1, 1) irányába, a gradiens vektor és a vektor. Hasonlítsa össze a változás mértéke funkció ezeken a területeken.
Határozat. Annak érdekében, hogy megtalálják a származékos irányába a vektor első megtalálja a nagyságát és iránykoszinuszokat.
Megtaláljuk a parciális deriváltjai a függvény pont:
A deriváló funkcióihoz a vektor irányát:
Mi vektor megalkotására gradiense a talált részleges származékok azon a ponton, M és megtalálja a modul:
ez várható.
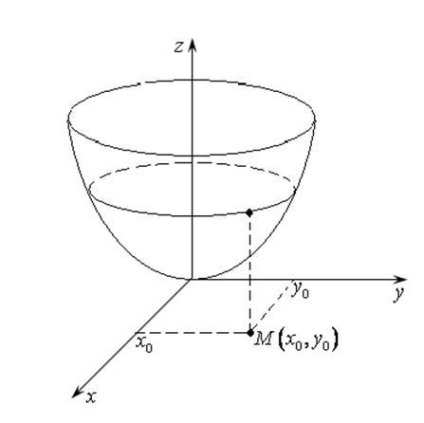
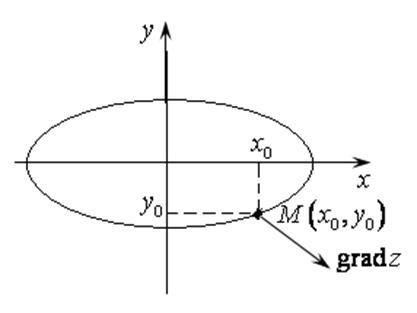
Ha a függvény olyan függvény két változó, a vektor
azon a ponton fekszik a HOT sík és merőleges arra a felületre, a vetítési metszősík párhuzamos HOY. (Ábra. 16,5).
16.7. következtetés
Felhívjuk az első következtetéseket a témában.
1. törvény változása egy változó U függően két vagy több egymástól független x változó. A stb Úgy hívják sok változó függvénye.
2. Változások U különböző változók különböznek egymástól, és az jellemzi, részleges származékok. Részleges származékok mutatják a változás mértéke az irányt.
3. A változás sebessége tetszőleges irányba jellemezve származékot ponapravleniyu vektor.
4. Az az irány, amelyben a sebesség legnagyobb, mivel a vektor, amelynek gradiens egy különleges nevet. A pont koordinátái megegyeznek az érték a parciális deriváltak ezen a ponton, és a modul - a változás mértéke.
Előadás 17.
Magasabb rendű származékok.
EKSTEMUM függvény két változó
9. részleges származékok nagyobb megrendeléseket.
10. Extrema a feladatokat a két változó.
11. A legnagyobb és a legkisebb érték a függvény a zárt térségben.
12. Kiválasztási paramétereket a tapasztalati képletek legegyszerűbb formája a legkisebb négyzetek módszerével
17.1. bevezetés
Abban a vizsgálatban, a függvények egy változó mellett a származékot az elsőrendű, amely jellemzi az változási sebessége egy folyamat, bevezettük a koncepció a második derivált, amely felelős volt a gyorsulás. Egy függvény a két változó, van két részleges származékok, amelyek általában szintén funkciói ugyanazok a változók, és ezért ismét, tudják különböztetni, és x. és y. Meg fogjuk mutatni, hogyan kell ezt csinálni.
17.2. Magasabb rendű származékok
Legyen a függvény z = f (x, y) folytonos azok részleges származékai és néhány régióban D HOY síkban.
Meghatározása 17.1.Chastnymi másodrendű (vagy a második részleges származékok) vannak az említett származékok és származékai.
A második részleges származékokat a következőképpen jelöljük:
Itt függvény egymás differenciált képest x kétszer;
Itt f differenciált képest x először. és akkor az eredmény az y;
Itt f különböztetni az első felett. és akkor az eredmény az x;
Itt f differenciált kétszer képest y.
Az első és az utolsó származékos néha tiszta. és a második és a harmadik - a kevert másodrendű származékok.
Be lehet bizonyítani (lásd. Kramer bemutató)), amely
azzal a feltétellel, folytonosság a származékok előre beállított pontot, azaz. e. a második kevert származékot nem függ a sorrendben a differenciálás, és ezért négy parciális származékokat redukálnak három.
Második származékok újra kell különböztetni mind x. és y. Kapunk harmadik deriváltak, kettő, amelyek tiszták, és a többi hat - vegyes:
Itt figyelembe vesszük, hogy
és így nyolc részleges négyre csökkentették.
Ez a folyamat is fogadja és származékai bármilyen sorrendben, feltéve, hogy azok a folyamatos egy előre meghatározott ponton.
Példa 17.1. Számítsuk ki a második deriváltak a függvény
Határozat. Azt találjuk, az első deriváltak, szem előtt tartva, hogy a részleges derivált az x a feltételezéssel számítva, hogy a - állandó és fordítva:
Mi található a második deriváltak
Példa 17.2. Dana funkciót. Mutassuk meg, hogy.
Határozat. Találunk egymás értékeit minden származéka, és ellenőrizze, ez az egyenlőség.
Mi helyettesíti az értékeket találtak az eredeti egyenlet:
Látjuk, hogy az egyenlet a megadott függvény fut le.
Példa 17.3. Dana funkciót. Mutassuk meg, hogy.
- a bal oldali.
Kiszámításához a megfelelő figyelembe venni, amit már ismert, és megtalálni
így eredeti egyenlőség a meghatározott feladatokat.
Mint látható a fenti példákból, akkor legyen éber, és szétválasztani a lehető legnagyobb mértékben azokat a változókat, amelyek ebben az esetben jár, mint egy állandó.
17.3. Szélsőértékében feladatokat a két változó
Megbeszéltük a szélsőséges egyváltozós függvényeket részletesen. Mi át ezt a tudást, hogy a funkció a két változó között.
Definíció 17.2. Point nevezzük maximum funkciót, ha
az összes pont (x, y) elegendően közel a pont, és attól elkülönülő (ábra. 17.1).
Definíció 17.2. Egy pont az úgynevezett minimum pont a funkciót, ha
az összes pont (x, y) kellően közel legyen a pont és elkülönült azokból. (Ábra. 17.2).
A pontokat, ahol a részleges származékok zérussal egyenlő vagy nem létezik, az úgynevezett kritikus.
Előfordul, hogy a pont a szélsőérték, és lehetséges, hogy meghatározza a jellegét a józan ész.
Például, a függvény minimuma van u, azaz az M pont (1,2). Valóban, minden első ciklus tovább fog növekedni, és a - szintén, tehát, azon a ponton, M (1.2) van a legkevesebb, a (17.1 ábra.).
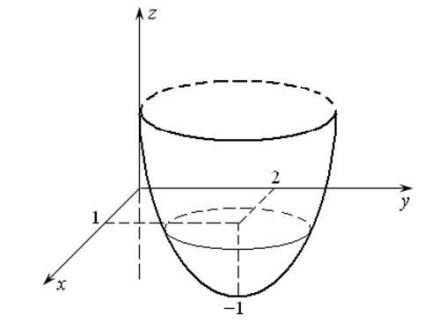
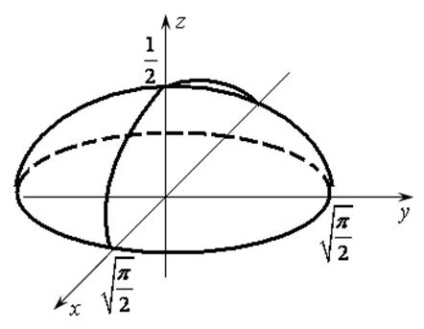
Funkció maximum a ponton (0,0), és a (ábra. 17.2).