Teljes bináris fa
bináris fa
A fák között bocsát ki speciális alosztálya úgynevezett bináris fák. Bináris fa - gyökeres fa, hogy minden egyes csomóponthoz legfeljebb két leányvállalata, gyakran egyértelműen rendelhető: balra és jobbra. Például, ez egy bináris fa:

Között bináris fák különíteniük teljes bináris fa. amelynek minden csúcsa van két leányvállalata, kivéve a leveleket, amelyek székhelye azonos mélységben:

Azt is gyakran nevezik a teljes bináris fa, amely teljesen megtöltötte a szinten, kivéve az utolsót:

Amikor 1-csúcsok indexelése keresztül fentebb megadott szintek, vannak egyszerű képletek közötti átmenet csomópontok. Egy csúcsból index $ v $ képlet származású balra, csökkenő jobbra, és emelje fel a következők szerint:
$$ L = 2V \\ r = 2v + 1 \\ p = \ left \ lfloor \ right \ rfloor $$
Ebben a tekintetben a teljes bináris fák gyakran tárolják nem formájában a szomszédsági lista formájában egy egyszerű tömb, ahol a $ tree [v] $ - hozzárendelt érték a felső index $ v $. A bejárás segítségével fenti képletek.
Meg kell jegyezni, hogy a magasság (szintek száma) teljes bináris fa $ N $ csúcsok értéke $ \ log N $. Ez a tulajdonság gyakran használják, hogy értékelje a komplexitás, a különböző algoritmusok.
Egy csomó (angol kupac.) - az egyik legegyszerűbb adatszerkezetek alapján a fák. Egy rakás fenntartására használják elemekből álló készlet, amely képes gyorsan megtalálja a maximális (vagy minimális, nem számít).
Klasszikus csokor a következő műveleteket támogatja:
- Elem hozzáadása (Nehézség: $ O (\ log N) $)
- Keresse meg a maximális (Nehézség: $ O (1) $)
- Kivonat a maximális elem (Nehézség: $ O (\ log N) $)
egy halom elemek formájában tároljuk a teljes bináris fa. Fő tulajdonság (a kupac invariáns) van megfogalmazva a következő:
Elem minden csomópont nagyobb vagy egyenlő elemek minden gyermek csúcsot.
Ebből az is következik, hogy a legkisebb elem mindig a gyökér a fa.
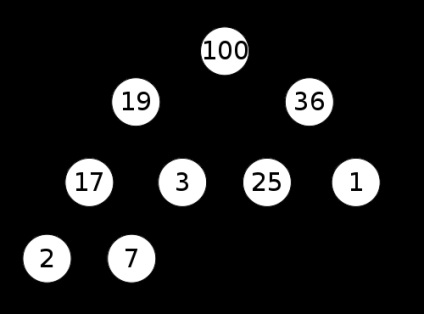
Ha hozzáad egy csomó új bejegyzés az első elérhető index. Ez azt jelenti, hogy a bináris fa van töltve a szintet, balról jobbra. Az adagolás befejezése után az elem lehetséges, hogy a kupac invariáns megszűnik végezni, mint egy új elem lesz nagyobb, mint a közvetlen őse. Ilyen esetekben egyszerűen cserélhető az elem a közvetlen őse. Ha a kupac invariáns még mindig nem elégedett, akkor változtassa meg a helyét egy új őse, és így tovább, amíg a kupac nem normális. Ez a művelet a rámenős felfelé.
Kibontásakor a maximális elem, akkor a következő trükköt: mozgassa az utolsó elem a kupac (a jobb szélső az utolsó szinten) a gyökér a fa helyett a távoli csúcs. Ez szinte biztosan sérti egy változatlan, mint az új „maximális” kevesebb lesz elemek gyermek csomópontok. Vessük össze a két gyermek elemek, válasszon egyet, és cserélt a jelenlegi „maximális”. Ismételjük meg ezt a folyamatot, amíg a invariáns nem áll helyre. Ez az úgynevezett push-down.
végrehajtás
A koncepció egy sorban prioritással
Hallja helyett a „csomó”, a „sornak”. A gyakorlatban ezek felcserélhetőek egymással, bár a különbség a érték még mindig jelen van.
A sorban elsőbbséget - egy absztrakt adatszerkezet, amely lehetővé teszi, hogy fenntartsák a sor elemeit, keresse meg és letölteni legalább belőle, míg egy csomó - konkrét adatok szerkezete alapján a teljes bináris fa. Bármilyen csokor egy prioritási sor, de nem minden sorban prioritást (elméletileg) egy halom (a gyakorlatban szinte bármilyen). Akkor végre támogatja a többszörös extrakció maximum egy egyszerű tömböt, akkor a műveleti bonyolultság $ O (N) $, de továbbra is kiemelt sorban.
(Ha még nem ismeri, objektumorientált programozás, a sorban prioritás - felület és egy csomó - egy osztály, amely végrehajtja azt.)
A sorban prioritást a szabványos C ++ library
A szabványos C ++ library kupac jelen végrehajtása, amely támogatja az összes műveletet a fent megadott. Ez az osztály std :: priority_queue
Az alapértelmezés egy csomó, hogy megtalálják a legnagyobb. Ahhoz, hogy a kupac megtalálja a minimum meg kell használni a típus std :: priority_queue