Tehetetlenségi nyomatéka egyszerű szakaszok
Számított áramkör tervezés
1) -body gerenda keresztirányú méretei sokkal kisebb, mint a hossza (gerenda-átfedés)
2) -body lemez, az egyik p-ek, amely sokkal kisebb, mint a másik két (átfedő tartomány, az I-gerenda alján)
3) A burkolóanyagnak -body által határolt íves felületek közötti távolság, amely sokkal kisebb, mint a görbületi sugara (Dome épületek, falak és tartályok falak)
4) -body tömb, minden dimenzióját ugyanabban a sorrendben (a platina és a híd támogatás)
Külső, belső erők
Úgy hívják a külső erők hatnak a test más szervek által. Ők vannak osztva koncentrált és elosztott.
F- koncentrált erő (kN)
Me- pár erők nyomatéka (kN · m)
Q- egyenletesen elosztott terhelés (kN / m)
Úgy hívják belső erők a szervezetünkben hatására a külső erők.
Kaotikusan elrendezett belső erők lehet hozni a fő vektor és a fő szempont.
Vegyünk egy fát a kaotikus alkalmazása a külső erők F1, F2, F3, F4
1) belül a fa hőn tartó rész tengelyére merőleges a rúd, amely elválasztja a gerenda a 2 A és B részek
2) kell dobni másrészről (A rész)
3) A leválasztott részek cseréje 6. belső erő tényezők
4) alkotják az egyenleteket 6
a. Σh = 0 → N
b. Σy = 0 → Qy
c. Σz = 0 → QZ
d. ΣMx = 0 → Mx
e. ΣMy = 0 → Saját
f. ΣMz = 0 → Mz
Ha bármely belső erő tényezők negatív lesz, meg kell változtatni, hogy az ellenkező irányba adni.
Statikus pillanatok szakaszok
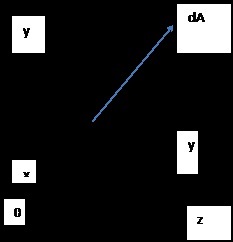

YDA - idő elemi terület tekintetében Oz
Zdá - idő elemi terület viszonylag Oy
Statikus pillanatok tengelyek körül y és z jelentése az úgynevezett integrálok
S - Statikus pillanatban (cm3)
Sz = y∫dA ∫ydA
Sy = z∫dA ∫zdA
Statikai szempont lehet negatív vagy pozitív, vagy nulla.
Statikus pillanatban egy komplex szám összege statikus pillanatok az egyszerűbb alkatrészeket.
Tehetetlenségi nyomatéka
Megkülönböztetni axiális, centrifugális és poláris tehetetlenségi nyomatéka.
A tengelyirányú tehetetlenségi nyomatékok a szerves: Iz = ∫y 2 dA
Iy = ∫z 2 dA (4 cm)
Poláris tehetetlenségi integrál integrál: I # 421; = ∫ # 421; ²dA
Centrifugális tehetetlenség az integrál: Dyz = ∫zydA
A centrifugális tehetetlenségi lehet pozitív, negatív és zérus.
Polar és axiális tehetetlenségi nyomatéka, csak pozitív.
Tehetetlenségi nyomatéka az elemi részek.
Iz = bh 3/12 Iz = bh 3/36 Iz = Iy = πd 4/64 Iy = πd 4/128
Iy = HB 3/12 Iy = HB 3/36 A = πd 2/2 Iy = hb³ / 36Iz = πd # 8308; / 128 Iz1 = 0.11r 4
A tehetetlenségi nyomatéka párhuzamos tengely körül
Ha Sz, és Sy = 0, a képlet formájában:
Iy # 8321; = Iy + b²A - párhuzamos átvitel képletű
Tehetetlenségi nyomaték tekintetében párhuzamos tengelyek összegével egyenlő a tehetetlenségi nyomaték utal középtengely és a terméket a S (négyzet) darabokat a négyzetes közötti távolság ezek a tengelyek.
A fő tengely fő tehetetlenségi nyomatéka
A tengely körül a tengelyirányú tehetetlenségi nyomatékok egy extrém érték, és a centrifugális pillanatok = 0, az úgynevezett fő tengelye tehetetlenség. A helyzet a fő tengelye tehetetlenség határozza meg: tg # 8322, # 945; = - 2Dyz / Iz-Iy
pozitív szög # 945; késleltette a z-tengely az óramutató járásával ellentétes irányban, amikor a fő tengely áthalad a súlypontja a keresztmetszet, a tengelyek nevezzük a fő központi tengelyek.
Axiális tehetetlenségi nyomaték utal elsősorban központi tengelyei nevezzük fő tehetetlenségi nyomatékok, és számítjuk az alábbi képlet szerint.
1) A hipotézis folytonosság: feltételezi, hogy az anyag kitölti a teljes összeget bocsátott
2) A hipotézis az egységesség és izotrópia: azt jelenti, hogy az anyagi tulajdonságok azonosak minden pontban és irányban
3) A hipotézis ideális rugalmassága: azt jelenti, hogy az anyag teljesen visszanyeri az alakját követően a terhelést eltávolítottuk
4) A hipotézise közötti lineáris összefüggés a stressz és a törzs: feltételezi, hogy a feszültség egyenesen arányos a törzsek
5) A hipotézis deformáció kicsi: feltételezi, hogy deformáció (maradék) képest csekély a méretei a test, és el lehet hanyagolni
Tervezésekor struktúrákat kell venni a keresztmetszeti méretei úgy, hogy azok nem haladják meg az úgynevezett, a képesítést. megkülönböztetni:
# 963; adm megengedhető normális feszültség
# 964; ADM - megengedhető nyírófeszültség
# 963; adm hozott rideg anyagok részeként a végső erő. # 963; adm = # 963; l / n1
A műanyagok része a folyáshatár: # 1004; # 1006 .adm; t / n # 8322;
n # 8321; és n # 8322, együtthatója biztonsági tartalék (és nagyobb, mint 1)
# 1006; ADM = (0,5-0,6) # 1004; adm
szilárdsági számítások
1. meghatározása feszültség. Erőpróbát
2. meghatározása keresztmetszeti méret
3. meghatározása a megengedett
Módszer kezdeti paraméterek
A módszer hátránya a közvetlen integráció hogy meg kell határozni a nagyszámú tetszőleges konstansok.
Ha a sugár n-szakaszok, akkor létre kell hozni, és oldja meg a rendszer 2n algebrai egyenletek.
Az eljárás kezdeti paraméterek függetlenül attól, hány állomás kell azonosítani két tetszőleges állandók.
E - rugalmassági modulus
Iz - a tehetetlenségi nyomaték Oz
# 965; - az eltérítési pontnál
# 965; 0 - kezdeti alakváltozás
# 952, egy - a kezdeti elfordulási szög
x - a távolság a sugár a forgó szelvény
Az integrációs állandók itt egyszerű jelentése: a kezdeti (az x = 0), az értékek a funkciója ismeretlen és származékai. Ezért a módszer az integráló differenciálegyenletek képlet alapján, és széles körben használják a szerkezeti mechanika, az úgynevezett módszer kezdeti paraméterek.
Az eljárás szerint a kiindulási paraméterek, a gerenda két részre van osztva. Behelyettesítve (12,38) a (12,39), megkapjuk a funkciója lehajlása rúdrészt I:
Véges differencia módszer
Az elhajlás az elemi gerendák
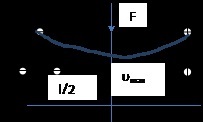
A tömített:
Bal - tömítő; jobbra - lefelé irányuló erő; alakváltozás - sima mozog 0 és tömítő az erő.
Bal - tömítő; az egész - egyenletesen megoszló terhelés mellett; kitérése mind az erő - a zökkenőmentes átmenetet le.
Rational gerendák
Ennek magyarázata az a rész, amely a legnagyobb erőt és a gazdaság.
A legtöbb normális hajlítási feszültségek alakulhatnak helyeken legtávolabb a z-tengely.
Minél közelebb Oz, a normál feszültség kisebb, és a tengelyen, akkor nullával egyenlő
És az anyag: a legnagyobb mennyiséget kell koncentrálni sokkal kevesebb.
Olajos anyagként I-alakú keresztmetszete van, amely arra szolgál, hogy a megítélése normál feszültséget, és a fal szolgál, hogy csatlakoztassa a polcok és az észlelés a tangenciális feszültségek, eredő hatására nyíróerők.
A sugár egyenletes szilárdságú
RSB nevezzük nyaláb keresztmetszetében, amely a maximális igénybevételt, minden szekció azonos, és megengedett
Forma RBS határozzuk meg a képlet:
Offset (szelet). alapfogalmak
Shift (cut) - forma a stressz-deformált állapotban, amelyben csak az egyik belső teljesítménytényező fordul keresztmetszetben.
Shear (vágott) számítjuk hegesztve csavarkötés, stb
Nyírási keresztmetszeti nyírási feszültségek alakulhatnak
Q - keresztirányú erő; A - keresztmetszeti terület
Veszélyes metszéspontjai
A veszélyek a pont legtávolabb a semleges vonal
A meghatározásuk végig a legtávolabbi pont a szakasz, hogy tartsa a vonalat párhuzamosan a semleges
Legtávolabb NL megy át egy veszélyes szakasz a pont
Számított áramkör tervezés
1) -body gerenda keresztirányú méretei sokkal kisebb, mint a hossza (gerenda-átfedés)
2) -body lemez, az egyik p-ek, amely sokkal kisebb, mint a másik két (átfedő tartomány, az I-gerenda alján)
3) A burkolóanyagnak -body által határolt íves felületek közötti távolság, amely sokkal kisebb, mint a görbületi sugara (Dome épületek, falak és tartályok falak)
4) -body tömb, minden dimenzióját ugyanabban a sorrendben (a platina és a híd támogatás)
Külső, belső erők
Úgy hívják a külső erők hatnak a test más szervek által. Ők vannak osztva koncentrált és elosztott.
F- koncentrált erő (kN)
Me- pár erők nyomatéka (kN · m)
Q- egyenletesen elosztott terhelés (kN / m)
Úgy hívják belső erők a szervezetünkben hatására a külső erők.
Kaotikusan elrendezett belső erők lehet hozni a fő vektor és a fő szempont.
Vegyünk egy fát a kaotikus alkalmazása a külső erők F1, F2, F3, F4
1) belül a fa hőn tartó rész tengelyére merőleges a rúd, amely elválasztja a gerenda a 2 A és B részek
2) kell dobni másrészről (A rész)
3) A leválasztott részek cseréje 6. belső erő tényezők
4) alkotják az egyenleteket 6
a. Σh = 0 → N
b. Σy = 0 → Qy
c. Σz = 0 → QZ
d. ΣMx = 0 → Mx
e. ΣMy = 0 → Saját
f. ΣMz = 0 → Mz
Ha bármely belső erő tényezők negatív lesz, meg kell változtatni, hogy az ellenkező irányba adni.
Statikus pillanatok szakaszok


YDA - idő elemi terület tekintetében Oz
Zdá - idő elemi terület viszonylag Oy
Statikus pillanatok tengelyek körül y és z jelentése az úgynevezett integrálok
S - Statikus pillanatban (cm3)
Sz = y∫dA ∫ydA
Sy = z∫dA ∫zdA
Statikai szempont lehet negatív vagy pozitív, vagy nulla.
Statikus pillanatban egy komplex szám összege statikus pillanatok az egyszerűbb alkatrészeket.
Tehetetlenségi nyomatéka
Megkülönböztetni axiális, centrifugális és poláris tehetetlenségi nyomatéka.
A tengelyirányú tehetetlenségi nyomatékok a szerves: Iz = ∫y 2 dA
Iy = ∫z 2 dA (4 cm)
Poláris tehetetlenségi integrál integrál: I # 421; = ∫ # 421; ²dA
Centrifugális tehetetlenség az integrál: Dyz = ∫zydA
A centrifugális tehetetlenségi lehet pozitív, negatív és zérus.
Polar és axiális tehetetlenségi nyomatéka, csak pozitív.
Tehetetlenségi nyomatéka az elemi részek.
Iz = bh 3/12 Iz = bh 3/36 Iz = Iy = πd 4/64 Iy = πd 4/128
Iy = HB 3/12 Iy = HB 3/36 A = πd 2/2 Iy = hb³ / 36Iz = πd # 8308; / 128 Iz1 = 0.11r 4