Téglalap, rombusz, négyzet 1
Négyszög sokszög, amely felsők $ 4 $.
A négyszög oldalai $ 4 $, $ 4 $ 4 és a $ csúcsszög $. Fél, hogy nincs közös csúcsa, az úgynevezett másik oldalon a négyszög, különben ezek az úgynevezett szomszédos. A szögek nem közös oldalak is nevezik szomszédos.
Most közvetlenül a definíció egy paralelogramma.
Paralelogramma - egy négyszög, amelyben ellentétes oldalai párhuzamosak egymással.
Idézzük alaptulajdonságait paralelogramma.
Az ingatlan 1: szemközti oldalak és sarkok a paralelogramma, illetve vannak kötve.
Az ingatlan 2: Átlós végzett paralelogramma felezik a metszéspont.
Tekintsük részletesebben téglalap fogalmak, rombusz és négyzet alakú.
téglalap
Paralelogramma, amely egy derékszögű, az úgynevezett egy téglalap (ábra. 1).
1. ábra téglalap
Nyilvánvaló, hogy a doboz mind a négy sarka egyenlő $ ^ 0 $
Tekintsük a következő két tulajdonságot a téglalap.
Az ingatlan 3: mindkét átlója egy téglalap egyenlő.
Legyen adott egy négyzet $ ABCD $. Döntetlen az átlós $ AC $ és $ BD $ (ábra. 2). Megmutatjuk, hogy $ AC = BD $.
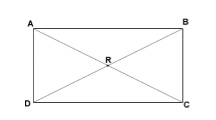
Mivel definíció, egy téglalap $ 1 $ egy paralelogramma, akkor az ingatlan az $ 1 $ paralelogramma, van
Mivel $ \ szög B = \ 'szög = ^ 0 $ és $ AB $ - gyakori mellékhatások, majd az egyenlőség elve alapján háromszögek I $ \ ABD háromszög = \ ABC háromszög $. ezért
Az ingatlan 4 (jellemző téglalap): Ha a két átló a paralelogramma egyenlő, akkor ez egy téglalap.
Legyen adott egy négyzet $ ABCD $. Felhívjuk átlós $ AC $ és $ BD $. Hadd találkozik egy ponton $ R $ (ábra. 2).
A tulajdon $ 2 $ paralelogramma és átlók egyenlőség, megkapjuk
Mivel $ \ szög DRC = \ angle ARB $, függőleges, akkor a $ i $ egyenlőség alapján háromszögek $ \ háromszög DRC = \ háromszög ARB $. Tehát $ \ szög RDC = \ angle RCD = \ angle RAB = \ angle RBA $.
Mivel a $ AB = AD $, akkor a háromszög $ ABD $ egyenlő szárú, valamint egy $ AE $ - Medián háromszög $ ABD $, $ AC $ merőleges $ BD $.
Téglalap, ahol mind a négy oldala egyenlő egymással, úgynevezett a tér (ábra. 5).
5. ábra tér
A tér - egy speciális esete rombusz. Következésképpen a téren az összes tulajdonságait egy téglalap és rombusz.
például probléma
Keresse meg a területet, a tér, az átlós amelyek 10 $ $.
Legyen az oldalon a tér által $ a $. Ezután szerint a Pitagorasz-tétel