Szorzás egy vektor egy szám - studopediya
Először is, a vektorok egy egyenesen vannak. Két vektor nevezzük esik. ha hazudnak ugyanabban a sorban vagy párhuzamos vonalak. Nagyjából elmondható, hogy beszélünk párhuzamos vektorok. De velük kapcsolatban mindig a jelzőt „egyenesbe”.
Képzeljünk el két kollineáris vektor. Ha a nyíl adatok vektorok vannak irányítva ugyanabban az irányban, az ilyen vektorokat nevezzük codirectional. Ha a nyilak a keresett különböző irányban, akkor a vektorokat ellentétes irányú.
Legend: kollineáris vektor levelet párhuzamosság ismerős ikon :. ahol részletezve: (kollineáris vektorok), vagy (ellentétes irányú vektorok).
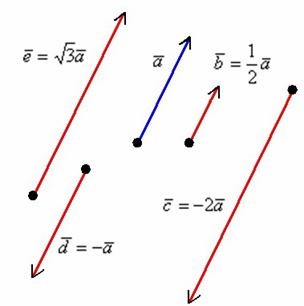
A terméket a száma nem nulla vektor olyan vektor. amelynek hossza egyenlő. Ezen túlmenően, a vektorok és kollineáris és ellentétes irányú a.
Szabály szorzás vektor számos könnyebb megérteni a segítségével a rajz:
9.Kollinearnye és koplanáris vektorok
Definíció. Vektor nevezzük esik. ha azok az azonos vagy párhuzamos vonal. A nulla vektor kollineáris bármilyen vektor. \
Definíció. A vektorokat nevezzük egy síkban vannak. ha van egy síkban, mindig parallelny.Kollinearnye vektorok egy síkban vannak, de nem minden egy síkban kollineáris vektor.
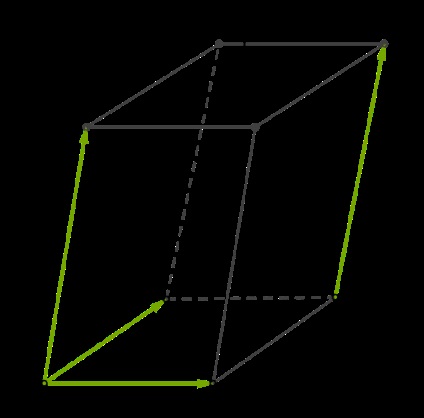
Az összes fenti esetben könnyű úgy, ha tesz az vektorok a széle a doboz.
1. Bármely két vektor egy síkban, de ugyanabban a síkban lehet helyezni és vektorok AA1- → -, CC1- → - és AD- → -, azaz a vektorok egy síkban vannak. Szintén egy síkban vektorok AA1- → -, AB- → - és CC1- → -, hiszen két ilyen vektorok párhuzamosak. Könnyen elképzelhető, hogy ha azokat a közös eredet, vektor CC1- → - egybeesik a vektor AA1- → -.
2. Például a vektorok ab- → -, ad- → - és AA1- → - nem egy síkban, mivel nem lehet elhelyezni ugyanabban a síkban.
Tünet coplanarity három vektor:
Hagyja, hogy a vektorok egy # 8407; és b # 8407; Nem esik. Ha a vektor c # 8407; csak egy pár valós számok x és y, így chtoc # 8407; = X # 8901; a # 8407; + Y # 8901; b # 8407;. akkor a vektorok egy # 8407;. b # 8407; és c # 8407; egy síkban vannak.
Ennek a fordítottja is igaz:
Ha a három vektor egy # 8407;. b # 8407; és c # 8407; koplanáris vektorok és a # 8407; és b # 8407; nem kollineáris, a vektor C # 8407; bővíthető szempontjából a vektorok egy # 8407; és b # 8407; egyetlen út.
10. A pont koordinátái koordinátái a vektor
Ha két pontot kapnak, és a gépet. A vektor a következő koordinátákat:
Adott két pont a térben és. A vektor a következő koordinátákat:
Azaz, a végén a vektor koordinátái, akkor vonjuk le a megfelelő koordinátáit az elején a vektor.
Ügyeljen arra, hogy megértsük a különbséget a pontok koordinátáinak és koordinátáinak vektorok:
A pontok koordinátái - ezek közönséges koordinátáit egy derékszögű koordináta-rendszerben. Elhalasztja a pont a koordinátarendszerben, azt hiszem, akkor is mindenki 5-6 osztályban. Minden pont egy szigorú hely a gépen, és mozgassa őket valahol máshol lehetetlen.
A koordinátákat a vektor - ez a terjeszkedés alapja. ebben az esetben. Bármilyen vektor ingyenes, így ha szükség van akkor könnyen elhalasztja azt néhány más pontján a gépet. Érdekes, hogy a vektorok lehetséges, hogy nem épít egy tengelyen derékszögű koordináta-rendszert igényel egyetlen alapot, ebben az esetben, ortonormált alapján a gépet.
Felvétel a pontok koordinátáinak és koordinátáinak vektorok hasonlónak tűnik :. és koordinálja a jelentése teljesen más. és szükség van egy jó megértése a különbség. Ez a különbség, persze, igaz tér
11.Koordinaty összege és különbsége vektorok, a termék számát
Hozzáadása vektorok (vektorösszege) a + b az a művelet számítási c vektor, amelynek minden eleme páronként összege a megfelelő elemek a a és b vektorok, azaz minden vektorelemet c egyenlő: ci = ai + bi
Kivonás vektorok (vektor különbség) a - b az a művelet számítási c vektor, amelynek minden eleme páronként különbségek a megfelelő elemek a a és b vektorok, azaz minden egyes eleme a c vektor adja meg: CI = ai - bi
Abban az esetben, a tér problémát összege és különbsége vektorok a = x; ay; AZ> és b = x; által; bz> megtalálható az alábbi képletek segítségével: