Szilárdságtani
Meghatározása után a kezdeti forgási szög kiszámítása alakváltozás szakasz A.
Megjegyzés. Elosztott terhelés q. ábrán látható szaggatott vonal 2.3 ábra bevezetjük azokban az esetekben, ahol az eltérítő határozzuk meg a keresztmetszet, amely kívül helyezkedik el a fellépés területe a megoszló terhelés.
Az elfordulási szög a szakasz képlettel számítjuk ki (2,20), amit meg kell tenni
Univerzális képletű Mora kiszámítására elasztikus elmozdulásai rúd rendszerek természetes általánosítása képletű Castigliano. Egy lineárisan rugalmas rúd rendszerek Castigliano formula formájában
ΔK generalizált elmozdulás szakasz K,
U függvénye potenciális energia.
A potenciális energia egy másodfokú erőfeszítést és hajlított elemek felírható
A legtöbb esetben a nyíróerő hatása a nagysága a potenciális energia elhanyagolják. Egyenleteket kombinálva (2,21) és a (2.22) ad
A parciális deriváltja a funkció megfelel a hajlítónyomaték tevékenysége által okozott egyetlen generalizált erő szakaszban K irányában a kívánt mozgást. Egyenlet (2,23) van írva a formájában
Ez határozza meg egy adott formáját univerzális képletet Mora meghatározásának vonatkozásában elmozdulás a hajlítási elemeket.
A gyakorlatban, egy grafikus-elemző értékelés az integrál Mora vétel (vétel Vereshchagin).
- a terület a rakomány diagram (diagramja a hajlítónyomaték a hatását egy előre meghatározott terhelés);
- koordinálja egyetlen rajz (a hajlítónyomaték diagramja az intézkedés az egység generalizált erő) szerint mérve a közepén a rakomány diagramok.
A számítás a szerves Mora képletű Vereshchagin a szakirodalomban az úgynevezett „megszorozzuk” diagramok.
Bizonyos esetekben, amikor kiszámításakor szerves Mora kényelmesen használható a képlet a Simpson
ahol az indexek „n”, „c”, „k” - rendre jelöli elején, közepén és végrész szorzótényezővei diagramok.
2. példa Annak megállapításához, a lehajlás a szakaszában és B. szakaszának a gerenda forgatási szög, tárgyalt 1. példa (ris.2.4.a).
A számítás a szerves Mora, hogy a képlet a Simpson.
Annak meghatározására, az eltérítő szakasz van kialakítva rakomány Mp (ris.2.4.b) és az egység (ris.2.4.v) hajlítónyomaték.
Szorzás a rakomány egység és nyomatéki ábrák Simpson formula adja
Az elfordulási szög az alátámasztó szakasz van kialakítva a második egység a hajlítónyomaték diagram a fellépés egység pillanatban alkalmazott metszetben tartóelem (ris.2.4.g).
A forgásszög úgy határozzák meg az egység és áruszállítás (ris.2.4.g) diagramok hajlítónyomatékokat.
Megjegyzés. A mínusz jel a válasz azt jelzi, hogy a tényleges mozgási irányával A és B lesz ellentétes a mozgás irányát megfelelő egyetlen általánosított erők.
2.3.Staticheski meghatározatlan gerenda
(Módszer redundancia nyitóerők)
Statikailag határozatlan tartók tartalmaznak „extra” kapcsolatot (ha felesleges linkeket gerendák statikailag meghatározható). A számos extra linkek határozza meg a mértékét redundancia probléma.
Statikailag határozott geometriailag megváltoztathatatlan gerenda nyert egy adott statikailag határozatlan eltávolításával felesleges kapcsolatok, az úgynevezett alap rendszer az erő módszer.
Algoritmus megoldására statikailag határozatlan gerendák által erők tartják a példa a statikailag határozatlan gerenda (ábra. 2.5.a).
Megoldás A probléma kezdődik a kiválasztás az alapvető rendszer az erő módszer (ábra. 2.5.b). Meg kell jegyezni, hogy ez nem az egyetlen lehetőség kiválasztását az alapvető rendszer (különösen a variáns törlését belső kapcsolatok beállításával a csukló).
A módszer lényege az erők, hogy tagadja mozgás az irányt a távoli kapcsolat. Matematikailag ez a feltétel felírható egyenlet mozgások kompatibilitás
δ11 - mozgását a csökkent kommunikációs irány, hatása által okozott, a fajlagos értékeket az ismeretlen távoli kommunikációs reakció (ábra 2.5.v).
Δ1R - felé a csökkent kommunikációs, által indukált egy adott terhelés (ábra 2.5.g).
Számítási δ11 mozgásokat. Δ1R által Simpson-féle képlet.
Együttható δ11 kanonikus egyenlet módszer erők határozzák meg, az egység diagram (ábra. 2.5.e) önmagára
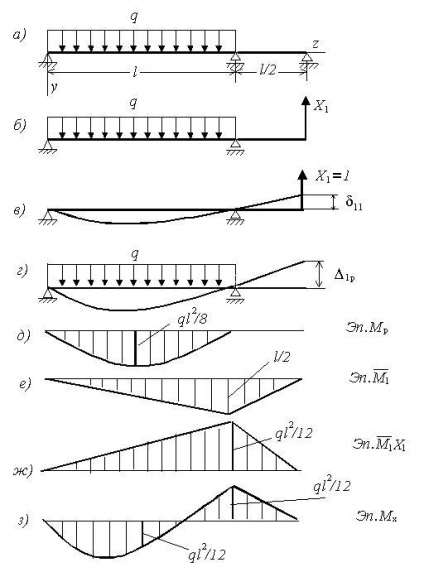
Együttható Δ1R kanonikus egyenlete az erő módszer szorzata az egység (ábra. 2.5.e) és teherautók (ábra. 2.5.d) diagramok
A egyenlet megoldása (2,27) úgy határozzuk meg, a reakció a felesleges kommunikációs X1
Ez a lépés megfelel a nyilvánosságra hozatala a határozat redundancia probléma.
A diagramja a hajlítónyomaték Mx (ábra. 2.5.z) egy statikailag határozatlan nyaláb szerint konstruált a képlet
Ábra. 2.5.zh bemutatott „korrigált” az egység diagram, minden koordinátáit, amelyek megnövekedett a X1-szer.
A figyelembe vett algoritmus megoldásokat statikailag határozatlan problémák alkalmas módszer az erők statikailag határozatlan problémák megoldások torziós terhelés alatt axiálisan ható, valamint a deformáció a rúd nehéz.
2.4.Ustoychivost tömörített rudak
Teljes megértése az építési együtt számításokat a szilárdság és merevség szükséges számításokat a stabilitását sűrített és sűrített hajlított elemek.
Mérnöki objektumok más, mint a tervezési terhelések ismertetését kiegészítő, nem biztosított a számítás, kis perturbációi képes előidézni deformáció a tárgy nem-projekt elemek (görbületi tengelye a dúcok, térbeli hajlító lapos hajlított elem). Ennek eredménye az expozíció további intenzitásától függ ható erők a szerkezeti elem. Minden olyan elem, van egy bizonyos kritikus terhelési érték, amely felett egy kis véletlen zavar okozza visszafordíthatatlan deformáció a projekthez nem. Egy ilyen állapot az objektum veszélyes.