Spline interpoláció - studopediya
A nagyszámú interpoláció csomópontok kell használni a magas fokú Interpoláló polinomok, amely megteremti némi kényelmetlenséget a számítás. Tudod elkerülni a magas fokú interpolációs polinom-interpoláció részes betörni néhány darab az építőiparban minden független interpolációs polinom. Azonban az ilyen interpoláció jelentős hátránya: a pontok különböző térhálósító Interpoláló polinomok nem folytonos első deriváltját őket, így, hogy megoldja a problémát, szakaszonként lineáris interpoláció segítségével egy speciális fajtája, szakaszonként polinom interpoláció - spline interpoláció.
Spline - olyan funkció, amely az egyes részleges intervallumban algebrai polinom-interpoláció és folyamatos a megadott tartományon együtt több a származékok.
Legyen az interpolált függvény f (x) határozza meg az értékeket a csomópontok. . Jelöljük a hossza a részleges szegmens. Arra törekszünk, egy spline minden részleges szegmensek formájában:
ahol - a négy ismeretlen együtthatók. Be tudjuk bizonyítani, hogy a problémát találni egy spline egyedülálló megoldás.
Egybeesni a értékek a csomópontokat az táblázatos függvény értékei:
Ezek száma egyenletek (2n) kétszer kisebb, mint az ismeretlenek száma együtthatók. Annak érdekében, hogy a további feltételek, akkor is szükség van a folyamatos első és második származékok spline minden pontján, beleértve a csomópontokat. Ahhoz, hogy ezt meg kell egyenlővé a bal és a jobb-származékok. . . a belső csomópontot.
Kiszámítása a kifejezés a származékokat. egymást követő differenciálódását (5,27):
megtalálni a jobb és a bal-származékok a csomópont:
Mi jár ezzel analóg módon történik a második derivált:
Egyenlővé balra és jobbra-származékok, ezt kapjuk:
Egyenletek (5,32) (5,33) ad egy további 2 (n-1) körülmények között. követelményeket szabhat a viselkedését a spline interpolációra végein a szegmens, hogy megkapjuk a hiányzó egyenletek. Ha a kereslet nulla görbületű végein egy spline interpolációs intervallumban (azaz, a második derivált nullával egyenlő), kapjuk:
Kizárva az egyenletek (5,28) - (5.33) n ismeretlennel. kapunk egy egyenletrendszert:
A rendszer (5,35) áll 3n egyenletek. Miután megoldotta a rendszerben (5,35), megkapjuk az értékeket az ismeretlen. meghatározzuk a készlet minden képletek a szükséges interpolációs spline
Program eljárás végrehajtására spline interpoláció meglehetősen nehézkes, ezért korlátozzuk a vitát, hogy megoldja a problémát interpolációs sine segítségével bordák segítségével MathCAD csomag jellemzői: interpolált (VS, x, y, z), lspline (x, y), pspline (x , y), CSPLINE (x, y).
Dokumentum csomag MathCAD, amely egy oldat spline, áll a következő blokkok.
1. Állítsa az asztal interpolált értékeket funkció
2. számítása spline együtthatók közeledik a határpont egy egyenes vonal, parabola, többtagú a harmadik fokozatot, ill.
3. Cél diszkrét rács értékeket számolja spline
Np: = 1000 i: = 0. Np Xi: = NP
4. számítása spline értékek a rácspontok
5. vizualizálása spline (ábra. 5.6)
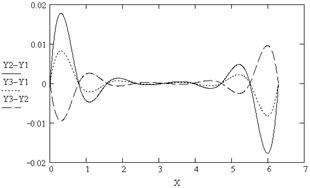
6. GFP- a különbség a spline különböző típusú a rács csomópontok (ábra. 5.7)
7. értékek kiszámítását az első származékok spline

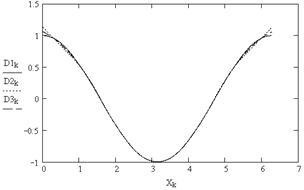
8. Plotting első származékok spline (ábra. 5.8)
9. kiszámítása értékeinek második származékok spline
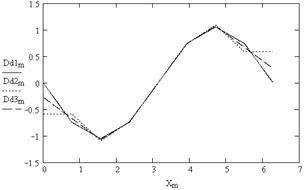
9. Plotting második származékok spline (ábra. 5.9)
10. kiszámítása az értékek a harmadik származékok bordák
11. ábrázolása harmadik származékok spline (ábra. 5.10)
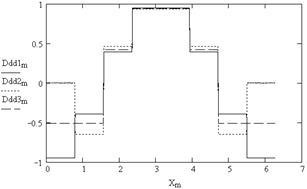
Amint az ábrából látható. 5,8-5,10, első és második származékok folyamatos spline függvények, harmadik és a magasabb rendű származékok - szakaszos funkciókat.