Polyhedra téglatest prizma piramis poliéder
Poliéderek. Prism, téglalap, piramis
Polyhedron - egy testet, amelynek a felületi áll véges számú n


A poliéder konvex, ha található egyik oldalán a sík minden egyes sík poligon a felületen
Ezek sokszögek úgynevezett arcok. oldalukra - élek, tetejükön - poliéder. Szegmensek összekötő két csúcsot, és ne feküdjön az egyik oldalán, az úgynevezett átlós a poliéder.
(Prism bázis) - szabályos sokszögek oldala párhuzamos rendre, és a fennmaradó felületek (AA1 B B1, C1 BB1 C, stb) - paralelogrammák párhuzamosak a síkkal vonal (AA1 és a BB1 és CC1, stb). . Paralelogrammák AA1 B1 B, BB1 C1 C, stb Ezek az úgynevezett keresztirányú széle van; bordák AA1. BB1. CC1 stb Úgy hívják oldalsó élek.
A magassága a prizma - bármilyen merőleges csökkent bármely pontjáról alapján az a másik alapsík.
Attól függően, hogy a sokszög alakú mélyén, a prizma lehet: háromszög, négyszög, ötszög, hatszög, stb
Ha egy bázist merőleges síkban az oldalsó széleit a prizma, egy ilyen prizma nevezzük egy egyenes vonal; Ellenkező esetben - ez a ferde hasáb. Az ábra mutatja a vonal és a ferde prizma
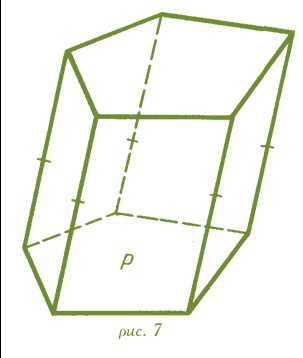

Ha tövénél egyenes hasáb egy szabályos sokszög. ilyen prizmát is nevezik a jobb oldalon.
1. A bázisok a prizma egyenlő sokszög.
2. kb. Az oldalsó felületei hasáb paralelogramma.
3. kb. Az oldalsó prizma élei egyenlő.
Egy doboz - egy prizma, amelynek bázisok paralelogramma. Így egy doboz hat oldala van, és minden - paralelogramma. Szemben arcok egyenlő és párhuzamos. A dobozban
négy átlós; mindannyian metszik egy ponton, és ossza félbe.

Ha a négy oldalsó felületei a doboz - téglalap, ez az úgynevezett közvetlen. Direkt egy doboz, amelyben mind a hat arcok - téglalapok, az úgynevezett téglalap. D átlója egy derékszögű paralelepipedon és a szélei a, b, c által összekötött kapcsolatban: d 2 = a 2 + b 2 + c 2.

Téglatest minden arcok terek, úgynevezett kocka. az

1. A dobozban 8 csúcsa, 12 éle, és 6 arcok.
2. kb. Minden arc a dobozban - paralelogramma.
3. kb. Homlokfal mezőben egyenlő.
4 kb. Párhuzamos élek a téglatest egyenlő.
Piramis - poliéder, amelyben egyik oldalán (az alapja a piramis) - egy tetszőleges sokszög (ABCDE, ris.80) és más arcok (oldalfelületek) - háromszögek egy közös vertex S, az úgynevezett csúcsa a piramis.
SO merőleges esett a tetején a piramis a talpára, úgynevezett vysotoypiramidy. Attól függően, hogy a sokszög alakú fekvő alapja a piramis lehet: háromszög, négyszög, ötszög, hatszög, stb A háromszög alakú piramis egy tetraéder (Tetrahedron), egy négyszögletes - pentaéder stb
Piramis úgynevezett helyes. ha az alap egy szabályos sokszög, magassága esik a központtól a bázis. Minden oldalélek jobb piramisok; valamennyi oldalirányú arcok - egyenlő szárú háromszög. A magasság az oldalfelületeken (SF) apothem úgynevezett reguláris piramis.

Ha költeni abcde listájában. az alappal párhuzamos ABCDE (Fig.81) a piramis, a test között kötött ezeket a sík és az oldalsó felületének az úgynevezett csonka gúla. Párhuzamos arcok ABCDE és ABCDE nevezik bázisok; távolság Oo közöttük - magasság. Csonka gúla úgynevezett helyes. Ha a piramis, ahonnan kaptuk - helyes. Minden oldala nézzen jobbra csonka gúla - egyenlő húrtrapéz. A magasság az oldalsó felület Ff
(Fig.81) nevezik apothem rendszeres csonka gúla.
Tulajdonságok rendszeres piramis
1. Az alapja egy szabályos piramis - szabályos sokszög.
2. kb. Oldalsó felületei szabályos piramis - egyenlő szárú háromszög.
3. kb. Az oldalsó széleit a piramis jobb.