Polinom hosszú körzet (terület)
Kezdjük néhány definíciót. Polinomja n-ed-fokú (vagy n-edik-sorrendben) lesz az úgynevezett kifejeződése formájában $ P_n (x) = \ sum \ limits_ ^ a_x ^ = a_x ^ + a_x ^ + a_x ^ + \ ldots + a_x + a_n $. Például, a kifejezés $ 4x ^ + 87x ^ 2 + 4x-11 $ egy polinom, amelynek mértéke 14 $ $. Meg lehet leírni a következőképpen: $ P_ (x) = 4x ^ + 87x ^ 2 + 4x-11 $.
$ $ A_0 tényezőnek nevezett vezető együtthatója polinom $ P_n (x) $. Például, a polinomiális $ 4x ^ + 87x ^ 2 + 4x-11 $ vezető együttható egyenlő $ 4 $ (számot, mielőtt $ x ^ $). A több $ a_n $ nevezzük konstans polinom $ P_n (x) $. Például, egy $ 4x ^ + 87x ^ 2 + 4x-11 $ $ konstans egyenlő (- 11) $. Most térjünk a tétel, amely szigorúan véve, és prezentációs anyagok alapján kerül sor ezen az oldalon.
Bármely két polinom $ P_n (x) $ és $ G_m (x) $ megtalálható például polinomok $ Q_p (x) $ és $ R_k (x) $, hogy a méltányosság végeznek
Az a kifejezés, "osztja polinom $ P_n (x) $ a polinom $ G_m (x) $" jelentése "a közölt polinom $ P_n (x) $ formájában (1)." Nevezzük polinom $ P_n (x) $ - osztható polinom $ G_m (x) $ - osztó polinom $ Q_p (x) $ - hányadosa $ P_n (x) $ a $ G_m (x) $, és a polinom $ R_k (x) $ - ostachey elosztjuk $ P_n (x) $ a $ G_m (x) $. Például, a polinom $ P_6 (x) = 12x ^ 6 + 3x ^ 5 + 16x ^ 4 + 6x ^ 3 + 8x ^ 2 + 2x + 1 $ és $ G_4 (x) = 3x ^ 4 + 4x ^ 2 + 2 $ nyerhető egy ilyen egyenlőséget:
Itt, a polinom $ P_6 (x) $ osztható a polinom $ G_4 (x) $ - osztóját polinom $ Q_2 (x) = 4x ^ 2 + x $ - hányadosa $ P_6 (x) $ a $ G_4 (x) $, és a polinom $ R_3 (x) = 2x ^ 3 + 1 $ - fennmaradó osztódó $ P_6 (x) $ a $ G_4 (x) $. Megjegyezzük, hogy a mértéke maradékot (azaz 3) kisebb, mint a foka az osztó (azaz 4), így a (1) egyenlet teljesül.
Ha a $ R_k (x) \ ekvivalens 0 $, akkor azt mondjuk, hogy a polinom $ P_n (x) $ elosztjuk a polinom $ G_m (x) $ nyom nélkül. Például, a polinom $ 21x ^ 6 + 6x ^ 5 + 105X ^ 2 + 30x $ osztható a polinom $ 3x ^ 4 + 15 $ nincs maradék, mint az egyenlőség:
Itt, a polinom $ P_6 (x) = 21x ^ 6 + 6x ^ 5 + 105X ^ 2 + 30x $ osztható; polinom $ G_4 (x) = 3x ^ 4 + 15 $ - elválasztó; és a polinom $ Q_2 (x) = 7x ^ 2 + 2x $ - hányadosa $ P_6 (x) $ a $ G_4 (x) $. A maradékot nulla.
Osztani a polinom egy polinom osztás gyakran használják az „oszlop”, vagy ahogy nevezik, „terület”. Megvalósítása ennek az eljárásnak Nézzük a példát.
Mielőtt megy a példák azt fogom bemutatni egy újabb ciklus. Ő nem általánosan elfogadott. és használja leszünk kizárólag a kényelem bemutatót. Amíg a végén ezt az oldalt fogják hívni egy magas rangú tagja a polinom $ P_n (x) $ $ kifejezést a_x ^ $. Például, a polinomiális $ 4x ^ + 87x ^ 2 + 4x-11 $ legidősebb elem $ 4x ^ $.
Osszuk $ 10x ^ 5 + 3x ^ 4-12x ^ 3 + 25x ^ 2-2x + $ 5 $ 5x ^ 2-x + 2 $, a szétválás "oszlopban."
Tehát van két polinom, $ P_5 (x) = 10x ^ 5 + 3x ^ 4-12x ^ 3 + 25x ^ 2-2x + 5 $ és $ G_2 (x) = 5x ^ 2-x + 2 $. Első fokú egyenlő $ 5 $, és a második fokozat egyenlő $ 2 $. Polinom $ P_5 (x) $ - az osztalék, és a polinom $ G_2 (x) $ - elválasztó. A mi feladatunk az, hogy megtaláljuk a hányados és a maradék. A feladat megoldható lépésről lépésre. Fogjuk használni ugyanazt a jelölést, hogy használják, hogy osztja a számok:
Senior polinom szakadék elem $ P_5 (x) $ (azaz $ 10x ^ $ 5) a vezető tagja a polinom $ Q_2 (x) $ (azaz $ 5x ^ 2 $):
A kapott expressziós $ 2x ^ 3 $ - ez az első saját elem:
Szorozzuk meg a polinom $ 5x ^ 2x + 2 $ a $ 2x ^ 3 $, míg a fogadó:
Írunk az eredmény:
Most vonjuk ki a polinom $ 10x ^ 5 + 3x ^ 4-12x ^ 3 + 25x ^ 2-2x + 5 $ polinom $ 10x ^ 5-2x ^ 4 + 4x ^ 3 $:
Töltse ki a polinom már a vonal alatt:
Ebben az első lépésben véget ér. Az eredmény, hogy kaptunk, felírható kibővített formában:
Mivel a polinom foka $ 5x ^ 4-16x ^ 3 + 25x ^ 2-2x + $ 5 (azaz, 4) nagyobb, mint a polinom foka $ 5x ^ 2-x + 2 $ (azaz, 2), a folyamat kellene, hogy továbbra is osztódó. Térjünk át a második lépésben.
Most fog működni a polinomok $ 5x ^ 4-16x ^ 3 + 25x ^ 2-2x + 5 $ és $ 5x ^ 2-x + 2 $. Hasonlóképpen, mint az első lépésben, elosztjuk az vezető tagja az első polinomot (vagyis $ 5x ^ 4 $) a fő elem a második polinomot (vagyis $ 5x ^ 2 $):
A kapott expressziós $ x ^ 2 $ - ez a második privát tagja. Mi hozzá a privát $ x ^ 2 $
Szorozzuk meg a polinom $ 5x ^ 2-x + 2 $ az $ x ^ 2 $, míg a fogadó:
Írunk az eredmény:
Most a kivonáshoz polinom $ 5x ^ 4-16x ^ 3 + 25x ^ 2-2x + 5 $ polinomiális $ 5x ^ 4-x ^ 3 + 2x ^ 2 $:
Töltse ki a polinom már a vonal alatt:
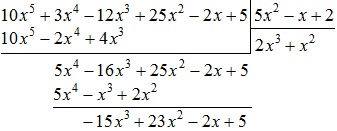
Ebben a második lépésben véget ér. Ez az eredmény felírható kibővített formában:
Mivel a polinom foka $ -15x ^ 3 + 23x ^ 2-2x + $ 5 (azaz, 3) nagyobb, mint a polinom foka $ 5x ^ 2-x + 2 $ (azaz, 2), majd folytatja a hasadási folyamat. Térjünk át a harmadik lépésben.
Most fog működni a polinomok $ -15x ^ 3 + 23x ^ 2-2x + 5 $ és $ 5x ^ 2-x + 2 $. Hasonlóképpen, mint az előző lépésekben, ossza el a vezető tagja az első polinomot (vagyis $ -15x ^ $ 3) a vezető elem a második polinomot (vagyis $ 5x ^ 2 $):
A kapott expressziós $ (- 3x) $ - ez a harmadik privát cellában. Töltsük ki a saját -3x $ $
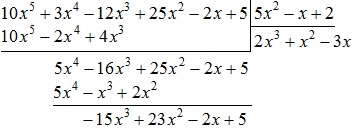
Szorozzuk meg a polinom $ 5x ^ 2-x + 2 $ a $ (- 3x) $, míg a fogadó:
Írunk az eredmény:
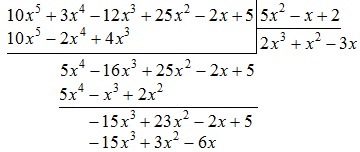
Most vonjuk ki a polinom $ -15x ^ 3 + 23x ^ 2-2x + 5 $ polinom $ -15x ^ 3 + 3x ^ 2-6x $:
Töltse ki a polinom már a vonal alatt:
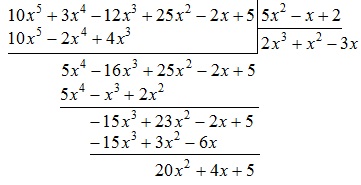
Ebben a harmadik lépésben véget ér. Ez az eredmény felírható kibővített formában:
Mivel a polinom foka $ 20x ^ 2 + 4x + $ 5 (azaz 2) egyenlő a polinom foka $ 5x ^ 2-x + 2 $ (azaz, 2), majd folytatja a hasadási folyamat. Térjünk át a negyedik lépés.
Most fog működni a polinomok $ 20x ^ 2 + 4x + 5 $ és $ 5x ^ 2-x + 2 $. Hasonlóképpen, mint az előző lépésekben, ossza el a vezető tagja az első polinomot (vagyis $ 20x ^ 2 $) egy vezető tagja a második polinomot (vagyis $ 5x ^ 2 $):
Az eredményül kapott szám $ 4 $ - ez a negyedik magán elem. Töltsük a privát $ 4 $
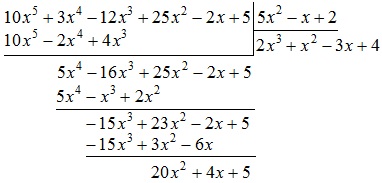
Szorozzuk meg a polinom $ 5x ^ 2-x + $ 2 $ 4 $, míg a fogadó:
Írunk az eredmény:
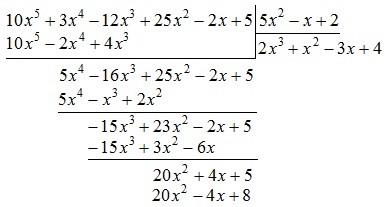
Most vonjuk ki a polinom $ 20x ^ 2 + 4x + 5 $ polinom $ 20x ^ 2-4x + $ 8:
Töltse ki a polinom már a vonal alatt:
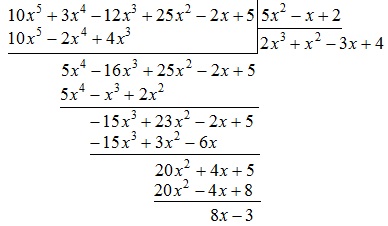
Ebben a negyedik lépésben véget ér. Ez az eredmény felírható kibővített formában:
Mivel a polinom foka $ 8x-3 $ (azaz 1) kevesebb, mint a polinom foka $ 5x ^ 2-x + 2 $ (azaz, 2), a szétválás folyamat befejeződött. A hányadosa polinom $ P_6 (x) $ polinommal $ G_2 (x) $ van a polinom $ Q_3 (x) = 2x ^ 3 + x ^ 2-3x + $ 4. A maradék a szétválás $ P_6 (x) $ a $ G_2 (x) $ - a polinom $ R_1 (x) = 8x-3 $. Sőt, már benyújtott eredeti polinom $ P_6 (x) $ formájában (1):
Válasz. elosztjuk - a polinom $ 2x ^ 3 + x ^ 2-3x + $ 4, a maradékot - a polinom $ 8x-3 $.
Osszuk $ 4x ^ 3 + 2x-11 $, hogy $ x + $ 5, a szétválás "oszlopban."
Használhatja a Horner rendszert (és nem lenne egy kicsit kevésbé nehézkes). Ahhoz azonban, hogy pusztán demonstrációs célokra használjuk az osztály „oszlopban.” Részletes magyarázatok a példában №1, ezért itt csak megemlítjük során a megoldás.
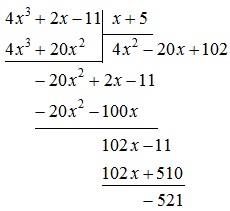
Az eredmény ebben a formában íródott:
Következésképpen, a hányadosa $ 4x ^ 3 + 2x-11 $ 5 $ x + $ van a polinomiális $ 4x ^ 2-20x + $ 102, és a maradék az a szám, $ (- 521) $ (sőt, ez egy polinomja érdekében nulla ).
Válasz. Private - polinom $ 4x ^ 2-20x + 102 $, a többi - a szám a $ -521 $.
Osszuk $ 7x ^ 3 + 9x ^ 2-5x + $ 9 $ 5x ^ 7 + 10x ^ 6-17x ^ 2 + 14x-7 $.
A mértéke az osztó (vagyis a polinom $ 5x ^ 7 + 10x ^ 6-17x ^ 2 + 14x-7 $) $ 7 $ egyenlő. A mértéke az osztalék (a polinom $ 7x ^ 3 + 9x ^ 2-5x + $ 9) = 3. Ebben a helyzetben, amikor a mértéke az osztó osztható nagyobb mértékben (7 $> $ 3) bomlása formában (1) csak akkor lehetséges, a következő formában:
Válasz. Magán a 0, a maradék - $ polinomiális 7x ^ 3 + 9x ^ 2-5x + $ 9.