Példák a módszerek problémák megoldására Euler diagram
A használata grafikai megoldások matematikai problémák használta Gottfried Vilgelmom Leybnitsem, a híres német matematikus és filozófus. A fejlesztés téma logikus volt, hogy megoldja a matematikai és gazdasági problémák a munkálatok Leonardo Eylera, a híres tudós a svájci származású, aki nagy hozzájárulását a fejlesztési magyar tudomány.
Egyes feladatok algebra több készlet könnyebb megoldani bemutatásával őket egy geometriai forma. Az ábra világosan mutatja, hogy a homogén és vegyes mennyiséget. A szabad része a kör egységes, kivetését a kör - vegyes.
Nézzük a példát a probléma a használata Euler körökben.
Két ötödik osztályban 50 gyermek. A színházi workshop run - 28, énekelni a kórusban - 33, sportolni - 23. Ezen túlmenően, a színház és az éneklés rabja 11 diák, a sportolók, hogy a kórus menni 4 és részt vesznek produkciók 9. Ez a 3 gyerek talál időt, hogy részt vegyen mindhárom bögre. Kiszámítja, hogy hány diák jár csak a kórus, színjátszó, a sport rész? hány gyermek nem tett semmit, kivéve tanulmányt?
A rajzon körök Euler látható eloszlás:
A színházi tartalmaz egy kört - 28, kör Hor - 33 Sport tartományban - 23;
körök metszik, és ha a teljes területet, a kör szerepel, a megfelelő számadatok között a színház és a kórus - 11, a sport és a kórus - 4 között a színház és a sport - 9;
belépünk az aktív területén metszi a három kör - 3.
Szerint a számok azt mutatják, hogy:
- Igaz sportolók 4/9/23 = 10
- színház - 09.11.28 = 8
- jövő énekesek 11/04/33 = 18
Megjegyzés: a átfedési terület mindhárom körökben. Ábra azt el kell osztani a körök száma 3 3 = 1.
Most lehet számítani a gyermekek száma, akik nem tartoznak a körök hobbi. Ehhez hozzáadjuk a homogén mező körök és vonjuk ki a gyermekek száma.
(Az első számjegy a központ a rajz)
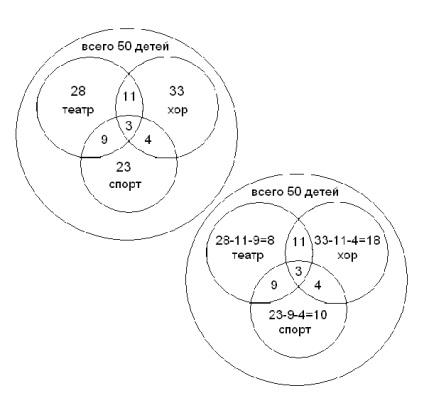
Válasz: részt vesz a színházi kör 8 gyerek a kórus - 18 gyermek, sport - 10, nem vesznek részt a körök 11 gyermek.
Logikusan, akkor újraszámolja a hallgatók. Látogasson mindhárom klub, tizenegy - nem, nyolc színház, tíz és tizennyolc sportolók énekesek, összesen 50 diák.