Az eljárás hurokáramok példák problémamegoldás
Minden áramkör, vannak az úgynevezett P - bordák (ezek ága egységek, területek) és Y - egységek. Leírni, van egy egyenletrendszert, amelyben a két Kirchhoff szabályokat alkalmaznak. A velük, mint független változók, amelyek a jelenlegi élek. Ezért a független változók száma megegyezik a számú egyenlet, amely lehetővé teszi a normál felbontású a rendszer.
A gyakorlatban bizonyos technikákat alkalmaznak, hogy csökkentsék a számát egyenletek. Közülük igen gyakran alkalmazott módszer a hurokáramok, lehetővé teszi, hogy végre bonyolult számításokat, és szerezzen egy meglehetősen pontos eredményt.
A módszer a hurokáramok
Az alapelvek A módszer azon a tényen alapul, hogy a fellépő bordák áramkör áramlatok, nem minden tekinthető függetlennek. A rendszerben jelen lévő Y-1 egyenletek a csomópontok, világosan mutatják a függőség ezen U-1 áramok. Elosztása során az elektromos áramkört független az aktuális P-V + 1, az egész rendszer lehet csökkenteni a egyenletek P-V + 1. Így, háló elemzés egy nagyon egyszerű és kényelmes választó áramkör áramok független P-V + 1.
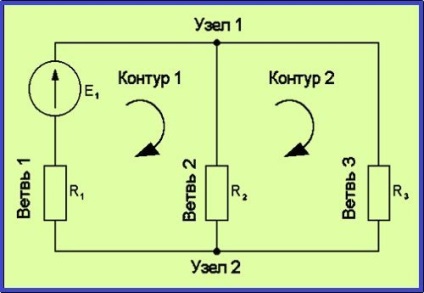
Ez a módszer lehetővé a számítás, hogy minden egyes független áramkör R-Y + 1 cirkuláltatjuk adott virtuális kör árama között. Ha bármelyik szélén csak egy bizonyos kör, az értéke átfolyó egyenlő lesz az igazi aktuális kontúrt. Abban az esetben, ha a széle része a többszörös körök, a jelenlegi benne áramló, összege lesz, beleértve a kontúr megfelelő áramot. Ebben az esetben meg kell vennie az irányt a kontúr körül. Független áramkörök átfedi szinte az egész pályán, úgyhogy az áram bármilyen szélén fejezhető ki az hurokáramok teszik ki a teljes rendszert az áramlatok.
Annak érdekében, hogy létrejöjjön egy olyan rendszer független áramkörök, egy egyszerű és intuitív módszer egy síkbeli gráf. Ebben a rendszerben elágazások és a csomópontok vannak elrendezve egy síkban oly módon, hogy a kölcsönös metszéspontja a bordák teljesen kiküszöbölhető. Ezzel a módszerrel, a gép van osztva régiók által határolt zárt élek lánc. Hogy azok a rendszer független hurkok. Ez a módszer a legalkalmasabb a kézi elszámolási rendszereket. Azonban annak használata válhat nehéz vagy lehetetlen, ha a vizsgált rendszer nem fér bele a keret egy sík gráf.
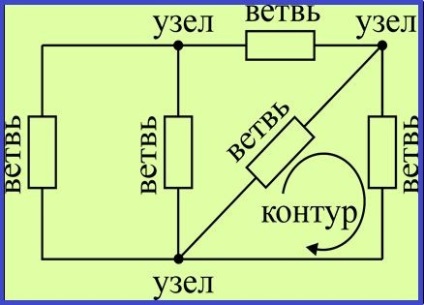
Egy másik módszer a számítás módszerét elosztása maximális fa. A fa maga képviseli, mint egy része az áramkör egységek és egyszerűen összefüggő gráf nem tartalmaz semmilyen zárt hurkok. Annak érdekében, hogy látom, mert a lánc fokozatosan megszűnik néhány link. Wood a maximumot, ha hozzá kizárt kapcsolat van, ezáltal egy hurkot.
A módszer alkalmazása elkülönítésére maximális fa egy szekvenciális áramkör kivételével előre egységek bizonyos szabályoknak megfelelően. Minden lépés a lánc állítólagos önkényes kizárása egy link. Ha ilyen kivételek ad egyszerű csatlakoztathatóság grafikon, felosztva azokat két különálló részből áll, ebben az esetben a kapcsolat lehet visszatérni az áramkörbe. Ha a gráf egyszerűen csatlakoztatva, akkor a link kizárt. Végső soron, az egységek számát, hogy ki vannak zárva a lánc, egyenlő az alkalmazott önálló áramkörök száma, elrendezve az áramkör. Termelés minden egyes új, független áramkör kapcsolatos kapcsolatot az elektromos áramkört a kizárt adott link.
A módszer alkalmazása kiszámítására a hurok áramkör
Összhangban ezzel a módszerrel, az ismeretlen mennyiségek számítjuk vagy kontúr áramlatok, feltehetően zajló összes független áramkörök. Ebben a tekintetben minden ismeretlenek és az egyenletek áram a rendszer megegyezik a független hurkok áramkört.
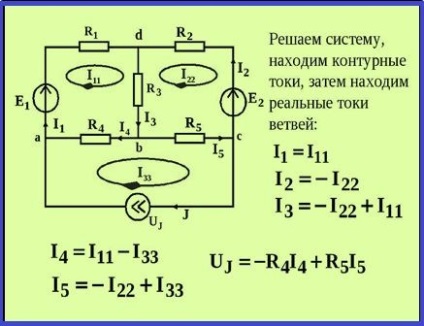
A ágak áramát összhangban ezzel a módszerrel számítása a következő:
- Elsősorban kapcsolási rajz készül a kijelölése annak valamennyi elemét.
- Következő van és meghatározza az összes független áramkörök.
- Útvonal áramlási hurok áramok önkényesen az óramutató járásával megegyező vagy azzal ellentétes irányban az egyes önálló áramkör. Ezek segítségével azonosítjuk digitális vagy karakterek.
- Összhangban a második törvénye Kirchhoff érintő kontúr áramok húzott egyenleteket minden független áramkörök. Az egyenlőség a rögzített hurok bejárás irányát és hurokáramot ugyanazt az áramkört. Meg kell figyelembe venni azt a tényt, hogy az ágak közelében áramló saját kontúrt áramlatok. Az esés fogyasztói feszültség külön-külön az egyes aktuális.
- A következő lépés az, hogy megoldja a kapott rendszer bármely szokásos módszerrel, és a végső meghatározása hurokáramok.
- Meg kell határozni az irányt a tényleges áramok minden ágában és megjelöli az egyes jelek, nem tévesztendő össze a kontúrt.
- Ezután mozgassa a jelenlegi kontúrt az aktuális, az a feltételezés, hogy az érték a jelenlegi valós szakági kontúrt algebrai összege átfolyó áramok ezen ága.
Ha a hurokáram iránya egybeesik az irányt a valódi hatalom, a matematikai jel nem változik, ha az algebrai összegzésével. Ellenkező esetben a hurok aktuális értéket meg kell szorozni -1.
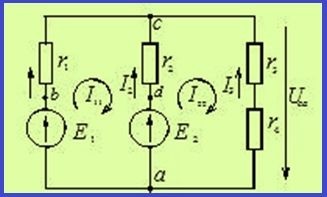
Módszer hurokáramok nagyon gyakran kiszámításához használt összetett áramkörök. Például a fenti séma kell állítania a következő paramétereket: E1 = 24V, E2 = 12 V, R1 = R2 = 4 ohm, r3 = 1 ohm, R4 = 3 ohm.
Ahhoz, hogy megoldja ezt a nehéz probléma két egyenlet megfelelő két független áramkör. Az irány a hurok áramok óramutató járásával megegyező irányban, és jelzi I11 és I22. Alapján a második Kirchhoff törvénye elkészíteni a következő egyenleteket:
Megoldása után a rendszer az áramok kapott kontúros értéke I11 = I22 = 3 A. Továbbá önkényesen jelöljük aktuális áram irányban I1, I2, I3. Mindannyian ugyanabban az irányban - függőlegesen felfelé. Ezt követően, az átmenet a kontúr a valódi. Az első ág csak egy hurok t aktuális I11. A iránya egybeesik a tényleges aktuális, így I1 + I11 = 3 A.
A továbbiakban egy valódi áram a második ág végzett két I11 és I22 hurokáramok. jelenlegi I22 iránya egybeesik a valós és I11 ellenkező irányba szigorúan valóságos. Ezért, I2 = I22 - I11 = 3 - 3 = 0 A. A harmadik ág I3 figyelhető csak a hurokáram I22. Irányának ellentétes irányt a valódi hatalom, így ebben az esetben a számítások a következők: I3 = -I22 = 3a.
Az alapvető módszer pozitív minőségi hurokáramok képest számítások szerint Kirchoff törvényei, sokkal kisebb számú egyenlet használt számítástechnika. Mindazonáltal léteznek olyan nehézségeket. Például, az igazi ágak áramát nem mindig lehet megállapítani, gyorsan és nagy pontossággal.