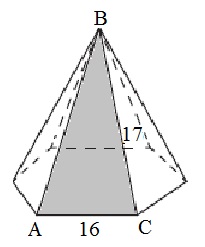
Oldalán az alap szabályos hatszög piramis 16 oldalszélei azonos nagyságúak 17

Oldalán az alap szabályos hatszög piramis 16 oldalszélei azonos nagyságúak 17. Találd meg a területet az oldalsó felületén a piramis.

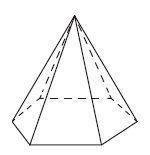
Mivel a piramis helyes, akkor az alapja egy szabályos hatszög, akkor az összes bázist összekapcsolódnak, és az oldalsó felületének a piramis áll hat egyenlő egyenlő szárú háromszög, amelynek bázisok 16 és az oldalsó - 17.

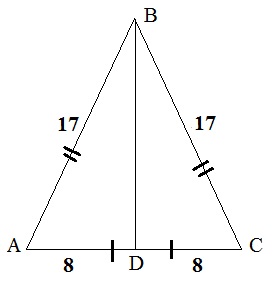
Ahhoz, hogy megtalálja az elején a terület egyik oldalán arcát. Ehhez figyelembe vesszük ABC egyenlő szárú háromszög (lásd. Az alábbi ábrát). Tudjuk, hogy a terület egy egyenlő szárú háromszög egyenlő a termék magasságának fele hosszának a $ S = \ frac \ cdot a \ cdot h $. A hossza a bázis, tudjuk, meg kell találni a magasságot.

Az ABC háromszögben tudjuk alapján ez a 16. Döntetlen a magasságot, hogy az alap, mint egy egyenlő szárú háromszög magassága a medián, akkor megosztja a bázis fele. Ezért AD = DC = 8. A Pitagorasz-tétel, azt látjuk, a magassága a BD:
\ [AB ^ = BD ^ + AD ^ \]
\ [17 ^ = BD ^ + 8 ^ \]
\ [BD ^ = 225 \]
\ [BD = 15. \]

Most helyettesítheti a számértékek a képlet megtalálása területén egy egyenlő szárú háromszög:
\ [S = \ frac \ cdot 15 \ cdot 16 = 120. \]

Korábban azt írta, hogy az oldalsó felület a piramis áll, hat egyenlő szárú háromszögek, akkor megtalálja a területet az oldalsó felületén a piramis, meg kell szorozni a területet egy egyenlő szárú háromszög (egyik oldalán felület) 6: 120 $ \ cdot 6 = 720 $