Megtaláljuk a távolság a párhuzamos vonalak egy síkban
A távolság két párhuzamos, egyenes vonal - a távolság tetszőleges pontja egyik párhuzamos vonalak a másik vonal.
Grafikusan ábrázolják a két párhuzamos vonal a és b, megjegyezzük, a vonalon, mint egy tetszőleges pont M1, M1 csepp a merőleges egy pont az egyenesen b, jelölő annak H1. M1H1 szegmens felel meg, a távolság a párhuzamos, egyenes vonalak a és b.
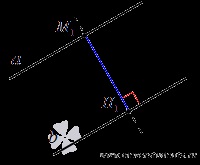
Ez a meghatározás a távolságot két párhuzamos vonal érvényes párhuzamos vonalak egy sík, valamint a közvetlen háromdimenziós térben. Ráadásul egy ilyen meghatározását a távolság a két párhuzamos vonal elfogadott véletlenül. Ez szorosan kapcsolódik a következő tétel.
Minden pont a két párhuzamos vonal eltávolítják az azonos távolságra a másik egyenes.
Tekintsük a párhuzamos vonalak a és b. Megjegyzés egy pontot az egyenesen M1 kihagyja azokból merőleges a b vezetéken. Az alap e merőleges jelöli H1. Ezután M1H1 merőleges távolság közötti távolság a párhuzamos, egyenes vonalak a és b, definíció szerint. Azt bizonyítja, hogy egyébként. ahol M2 - tetszőleges közvetlen pont egy, egy ponttól különböző M1, és a H2 - a bázis a merőleges levonni a pont M2 a vonalon b. Bizonyítva ezt a tényt, és bizonyítjuk a tételt is.
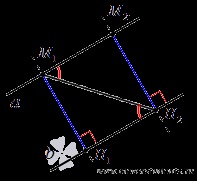
Mivel a belső keresztben fekvő szögek által alkotott metszéspontja két párhuzamos vonal egymást metsző, egyenlő (ez a cikkben tárgyalt párhuzamos vonalak párhuzamosak a vonal), majd a. és közvetlen M2H2, merőleges b építkezés által merőleges vonal és a. Ezután a háromszögek M1H1H2 M2M1H2 és téglalap alakú, és ráadásul, azok mentén átfogója, és hegyesszöget: M1H2 - közös átfogója. A egyenlőségét háromszögek egyenlő legyen a megfelelő oldalai, így. Ez azt bizonyítja, a tétel.
Meg kell jegyezni, hogy a távolságot két párhuzamos vonal a legkisebb távolságok pontok egy sort a másik vonalon pontokat.
Megtaláljuk a távolság a párhuzamos vonalak - elmélet, példák és megoldások.
Így, megtalálása közötti távolság a párhuzamos vonalak csökken megtalálása a hossza egy merőleges pontig húzott az egyik vonal a másik vonalon. Ebben az esetben ez választott módszert találni a távolságot. A választott módszer attól függ, hogy a körülmények egy adott feladatot. Bizonyos esetekben, akkor a Pitagorasz-tétel, mások - a jelek egyenlőség vagy hasonlósága háromszögek, meg a szinusz, koszinusz vagy érintő, stb Ha párhuzamos vonalak vannak megadva derékszögű koordinátarendszerben, a távolság a párhuzamos vonalak adott ki lehet számítani koordinátákat. Rajta és megáll.
Megfogalmazzuk a feltételeket a problémát.
Tegyük fel, hogy a repülőgép vagy a háromdimenziós térben rögzített derékszögű koordináta-rendszert, mivel két párhuzamos egyenes vonalak a és b, és szükség van, hogy megtalálja a távolságot ezeket a sorokat.
A megoldás erre a problémára meghatározásán alapul közötti távolság a párhuzamos vonalak -, hogy megtalálják a távolság a két adott párhuzamos vonal van szüksége:
meghatározzák a egy pont koordinátáit M1 feküdt a vonal egy (közvetlen vagy b);
kiszámítja a távolságot a pont M1 az egyenes vonalat b (vagy a).
Az előző pontban meghatározott M1 koordináta pont bármelyik beállított párhuzamos vonalak, nem probléma, kivéve persze, ha tudjuk, a főbb közvetlen egyenlet a gépen, és egyenest a térben egyenlet. Ahhoz, hogy megtalálja a távolságot az M1 a kívánt pontra a beállított párhuzamos vonalak hasznos lesz az Ön számára információkat szakaszban, hogy a távolság pont vonal.
Különösen, ha a derékszögű koordináta-rendszert Oxy síkot definiál egy egyenes vonal egyenletét általános formája. és közvetlen b, párhuzamos vonal, - általános egyenes egyenlete. közötti távolság ezek a párhuzamos vonalakat lehet képlettel számítják ki.
Megmutatjuk levezetése ezt a képletet.
Vesszük a lényeg. ami fekszik a vonal egy, akkor a pont koordinátáit M1 gyöke az egyenletnek. vagyis az egyenlőséget. ahonnan mi.
Ha. akkor a normális egyenes egyenlete b adott. és ha. akkor a normális egyenes egyenlete b adott. Ezután, amikor a távolság a pont a B vonal képlettel számítottuk ki. és amikor - az alábbi képlet szerint

Azaz, minden érték a távolság C2 pontról B vonal lehet kiszámítani a következő képlet szerint. És ha figyelembe vesszük, az egyenlőség. amelyet a fent kapott, ha a fenti általános válik. A következtetés az képlet a távolság a két párhuzamos vonal által meghatározott egyenletek általános közvetlen típus, és kész.
Nézzük megoldani a példákat.
Először is megtalálni a távolság a két párhuzamos vonal meghatározott derékszögű koordinátarendszerben a Oxy síkon.
Keresse meg a távolságot párhuzamos vonalak és.
Nyilvánvaló, hogy a sor, amelyek megfelelnek a paraméteres egyenleteket az egyenes vonal a nézet síkjával. Ez áthalad a ponton.
A kívánt távolság a párhuzamos vonalak egyenlő a távolság egy pont egy sorban. Mi kiszámítania.
Megkapjuk a szokásos egyenlet egy egyenes vonal, amely megfelel egy egyenes vonal egyenletét formájában a szögletes együtthatóval. Ehhez először írjuk általános egyenes egyenlete :. Most számítsuk ki a normalizációs tényező :. Megszorozzuk mindkét oldalán az egyenlet, van egy normális vonal egyenlete :. Keresek egyenlő távolság a modulusa egy kifejezés értékét. számított. Így, a távolság a párhuzamos vonalak egyenlő a beállított
A második oldatot.
Kapjuk egyenletekkel meghatározott párhuzamos vonalak.
Azt találtuk, hogy a vonal megfelel az általános egyenlet egy egyenes vonal. Mi jár a paraméteres egyenlete vonal típusát az általános egyenlet ezt a sort:

Az együtthatók az x és y az általános levezetett egyenletek párhuzamos vonalak egyenlő, így tudjuk közvetlenül alkalmazhatja a képletet a távolság a párhuzamos vonalak a gépen :.
.