Megoldás Közönséges differenciálegyenletek
A fegyelem „Számítógép
Megoldás közönséges differenciálegyenletek. Euler módszer
Közönséges differenciálegyenletek találhatók gyakran a különböző alkalmazások. Ezek a feladatok leírása pont mozgásának rendszerek, elektromos áramkörök és mások.
Úgynevezett differenciálegyenlet, amely kapcsolódik a független változó X, a funkcióját y = f (x) és származékai ezt a funkciót.
A implicit differenciálegyenlet van írva, mint:
Az, hogy a legmagasabb-származék, része ennek az egyenletnek nevezik a sorrendben a differenciálegyenlet.
Ha y = f (x) - függvénye a független változó X, egy közönséges differenciálegyenlet nevezzük, ha y = f (x1, x2, ... xn) - függvényében n független változók x1, x2, ... xn. akkor az egyenlet nevezzük parciális differenciálegyenlet.
Az oldatot egy közönséges differenciálegyenlet csökkenti a surf függvény az y = f (x), amely, ha szubsztituált egyenletbe felhívja be egy identitását.
A megoldás megtalálása ilyen egyenletet nevezzük az integráció, és az így kapott oldatot - a szerves ennek az egyenletnek.
Vannak általános és különösen megoldások a differenciálegyenlet.
Az általános megoldás az egyenletek egy olyan funkció y = # 966; (x, c), amely kielégíti az egyenletet bármelyik értéke konstans C.
A konkrét megoldás határozza meg az adott érték C. megtalálni egy adott megoldást kell adnia a kezdeti feltételek, azaz a az értéket a y, ha x = x0. azaz y0 = y (x0), ...,
A feladat olyan megoldás, hogy egy közönséges differenciálegyenlet a kezdeti feltételeket az úgynevezett Cauchy probléma közönséges differenciálegyenletek.
Úgy véljük, az egyenlet megoldható a legmagasabb származék.
Ezeket lehet csökkenteni, n közönséges differenciálegyenletek elsőrendű helyettesítésére ismeretlen funkciójú P1 (x), P2 (x), stb azaz
Ezen túlmenően, a kezdeti feltételek:
A megoldás, figyelembe vesszük a módszerek Euler és Runge-Kutta.
Numerikus megoldás az, hogy össze egy táblázatot a közelítő értékek y1, y2, ..., in-1 pontos megoldást y (x) egyenletet.
Nem tudjuk, hogy milyen típusú függvény, nem tudjuk közvetlenül kiszámítja a függvény értékét. Csak tudni, hogy a kezdeti feltételek, értékeit X0 = a, y0 = y (x0) és az intervallum [a, b], amely szükséges, hogy integrálja funkciót.
A problémát az alábbiak szerint történik: a pont X0, X1, ..., Xn találni közelítések y0, y1, ..., yn a pontos megoldás.
Az első lépés - szünet az intervallum véges számú rácspontok (rácspontok). hálókiosztás h = (b-a) / n, Xi = a + IH, I = 0,1. N.
Meg kell visszaállítani az értékek a funkciója ismeretlen. Tekintsük 1-sorrendben differenciálegyenlet
A második lépés - ismerve a kezdeti feltételek kiszámítjuk az érték az első derivált a ponton X0.
A harmadik lépés - a következő rácspont értékének kiszámításához a funkciót.
A negyedik lépés ismétlődik minden.
Geometriai értelmezése módszer abban áll, cseréje az integrál görbét egy szegmens rá tangenciális pontnál xi, yi. Minden lépésben ismét meghatározzuk a tangens, és ezért a közelítő megoldást a megfelelő görbe szaggatott vonallal. Ezért a módszer is nevezik szaggatott vonalak.
Reakcióvázlat számítás: xi = a + ih (I = 0,1, ..., N)
Ie amelynek ismert pont, a következőképpen számítjuk ki. Ez a számítás rendszere 1. egyenlet sorrendben.
Euler módszer egyenletek 2. érdekében szükséges egyenlet kezdeti feltételek csökkentik a rendszer két egyenlet az 1. szabály:
Származékok vett azon a ponton x.
Iteratív képlet:
A gyakorlatban, a számításokat végeznek alulról felfelé először értékeltük 1-származék, azaz pi. majd egy második Yi.
A másodrendű egyenletet kell alkalmazni kétszer integráció. Visszaállítása az érték a származékot, majd az érték a kívánt funkció, azaz Mi megoldjuk az első egyenletet, majd a második.
Példa. Az [a, b] hozzon létre egy táblázatot az értékek a közelítő megoldást a differenciálegyenlet. megfelel a kezdeti feltételek
Y (0) = 1, Y # 900; (0) = 2. integrációs lépésben h = 0,2, precíziós # 949 = 0,001. Ahhoz, hogy a pontos nyomtatási megoldásokat értékek y = e x + x.
Szükséges tömb X - X értékek 0 és 2
I - egy sor közelítő megoldások
F - egy sor értékek származék
(A-b) / h + első pont = 2 / 0,2 = 10 + 1 = 11
Figyelembe vett Euler módszer egy csoportjára utal egylépéses módszerek. ahol a számítás a pont (xi + 1 yi + 1) szükséges információt az utolsó számítási pont (xi. yi).
A numerikus megoldás az, hogy össze egy táblázatot a közelítő értékek y1. y2. y3. ..., in-1 pontos megoldást y (x) egyenlet y ¢ = f (x, y), egy £ x £ b a kezdeti feltétel y (x0) = y0. x0 = a kiválasztott szekvenciát pont a xi = x0 + IH. A funkció y függ az érv X
A pontosság vagy hiba megszüntetését hívás hiba, ami az átmenetet az előző a következő X, ha a differenciálegyenlet helyébe a kifejezést végtag.
A közelítési hiba egyenlő a differenciaegyenletek eldobjuk fennmaradó kifejezés a Taylor-sor O (h o +1).
Úgy vélik, ha a numerikus számítási módszer képletek összhangban vannak egy Taylor-sorfejtés szempontjából érdekében h o. p szám az úgynevezett rendjét módszer pontossági.
A számítási módszerét az Euler formula összehasonlítása a Taylor tágulási összhangban az első, hogy a h, azaz eljárás magában foglalja egy első sorrendű pontosságot lokális hiba O (h 2)
Az Euler módszer hiba h 2.
10.2. Numerikus módszerek az ábrázolási
A problémák megoldásához számítógépek elengedhetetlen láthatóság és könnyű gyors felfogása a jelenségek vizsgálata folyamatban van. Miután folyósítási grafikus üzemmód Turbo Pascal lehet építeni diagramok, valamint kapnak a különböző geometriai formák. Bármi legyen is a kép nem jelenik meg, akkor minden épült a pontokat, a csoport, amely viszont a szegmensek és görbék. Kimeneti pont eljárást elvégezni PutPixel (X, Y, szín), ahol a képletben X és Y-koordinátái a képernyő, ahol a pont található. Szín - a szín.
A konstrukció a grafikont a funkció az alábbi eljárással:
1) Tabulátor funkció;
2) meghatározása maximális és minimális értékek a függvény;
3) kialakulása és grafikus teljesítményt a képernyőn.
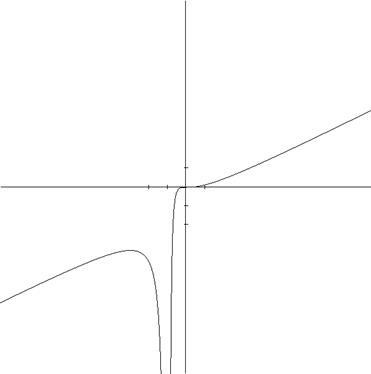
Tekintsük a használata a grafikus mód által az építőiparban a grafikon y (x) = x c / (2 (x + 1) (x + 1)) tartományba eső X Î [-5, -1) U (-1, 5] megnöveli H, és az épület aszimptotájának által adott expressziós Y (x) = x / 2 - 1.
Táblázatos formában funkciókat lehet megvalósítani a következő szereplők:
i. = 1-től n do kezdeni
Itt bemutatjuk a változó nevét: xStart - a kezdeti érték az az érv, Xe nd - a végső értéke az az érv, n - a pontok száma egy sorban. Lépés megváltoztatja az érv X képlet adja meg:
h: = (Xe nd-et -xStart) / (n - 1);
Egy hurok táblázatos funkciók számított értékek y (x), a rutin - egy funkció elemzi F. Az index minden egyes X értéke, és a megfelelő értéket az y (x), akkor kell fektetni bizonyos elemeit a tömb Y. Azon a ponton, x = -1 nem egy adott funkció meghatározva, ezért szükséges, hogy kizárják a rajzoló rész közelében ezen a ponton. Ezt úgy érjük el, szoftvert szereplők
ha y [i] <- 6 then y[ i ] := - 6;
Ebben az esetben ez elvégzett egy alsó határérték szintjén y = -6, és az összes érték, amely kisebb, mint -6, kizárásra kerül a rajzoló. Mintha a szomszédságában a különbség funkció kapna a pozitív érték lenne elvégezni a bevezetése egy felső határ szereplők
ahol a - határértéket.
Mértékének meghatározására a grafikonon, hogy meg kell találni a minimális és maximális értékek a tömb elemei Y. Ezt úgy érjük el szolgáltatók
i: = 1-től n-do kezdeni
ha y [i]> ymax majd
ha y [i] A telepítéshez a grafikus mód, akkor kell használni a szokásos eljárás InitGraph Graph modul, amely telepíti egyik lehetséges grafikus mód. eljárások következő formában: InitGraph (DriverName, mód put_k_drayveru); A Graph modul több mint 70 rutinok. Tekintsük a szükséges eljárások épület a grafikon Y = f (x) egy előre meghatározott tartományban variációs X egy előre meghatározott pályán h. Használja a következő eljárások kialakulásának moleno menetrend fejléc: SetTextStule (betűtípus, Direct, CharSize); -procedure kijelzőn megjelenő szöveg jelzi a betűtípust, és a döntés a mérete. betűtípust (betűtípus paraméter) a Graph modul meghatározza állandók: DefaultPont = 0 (mátrix típusú); TriplexPont = 1 (félkövér); SmallFont = 2 (kicsi); SansSerifPont = 3 (egyenes típusú); GothicPont = 4 (Gothic Font). Ahhoz, hogy meghatározzuk a a szöveg irányát használt kimenet állandók: Horizdir = 0 (balra) vagy VertDir = 1 (felfelé). A harmadik paraméter a betűméretet. Ha CharSize = 1, a szimbólumok a szokásos méretű (8x8 képpont), amikor CharSize == 2, a szimbólumok jelentése azonos méretekkel 16x16 pixel. A maximális értéke a konstans 10. SetTextJustify eljárás (kod_gorizontali, kod_vertikali) - beállítja a paramétereket adagolására a szöveget, attól függően, hogy a kódot. OutTextXY Eljárás (X, Y, szöveg); - olyan kimenetet biztosít a szöveget a koordináták (X, Y). Amikor képező X tengellyel, vízszintes és függőleges rácsvonalak használhatja a következő eljárást: SetLineStile (egyenes_típusa, opredelenie_polzovatelem / vid_linii); - határozza meg a vezeték típusa: solidin = 0 (folytonos vonal), dottein = 1 (pontozott vonal), centerin = 2 (pontozott vonallal), dashedin = 3 (szaggatott vonal), a felhasználó-bitin = 4 (a felhasználó által definiált vonal); A második paraméter csak akkor van értelme, ha userbitln = 4, és a nézet által meghatározott állandó vonal nonnwidth = 1 (normál vastagságú) vagy konstans thickwidth = 3 (folyamatos vonal); SetColor (szín) - határozza meg a színt a karakterek és vonalak. Ahhoz, hogy a kurzort az említett koordináta alkalmazott eljárás MoveTo, (X, Y), és a rajz egy sort az aktuális sor, hogy a megadott koordinátákat - az eljárás LineTo (X, Y). Ha képekkel dolgozik a használni kívánt koordináta-rendszerben. Attól függően, hogy a kiválasztott kép beállított mód képernyő felbontást 320x200, 640x480, vagy más képpontok száma (pixel). Szoftver által meghatározott maximális pixelek száma soronként keresztül GetMaxX funkció, és a sorok száma missing- keresztül GetMaxY funkciót. A származási beállítása (0, 0), a képernyő közepén - (GetMaxX div 2 GetMaxY div 2) és a jobb alsó sarokban - (GetMaxX, GetMaxY). Amikor teljesítményű grafikus műveleteket mindig jelezte, hogy azt kell, hogy a kurzort, de a kurzor maga láthatatlan grafikus módban.Kapcsolódó cikkek