Meghatározása a doboz, tulajdonságai - egy doboz - Geometria - Geometria - Matematika
II. szeterometria
1. meghatározása a doboz, annak tulajdonságait.
Van egy doboz úgynevezett prizma, amely az alapja paralelogramma.
Minden részletét a doboz - paralelogramma.
Mivel a doboz egy prizma, mind a tulajdonságok a prizma is érvényesek a dobozt.
Paralelepipedon, amelynek oldalsó szélei merőlegesek az alaplapra, az úgynevezett egyenes parallelepipedon. Ő oldalán arcok - téglalapok. Ábrán 459 mutat jobb paralelepipedon.
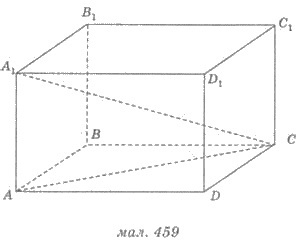
Ha az oldalsó szélei a paralelepipedon nem merőlegesek a bázis síkra, az úgynevezett ferde paralelepipedon. Ábrán 460 mutatja egy ferde paralelepipedon.
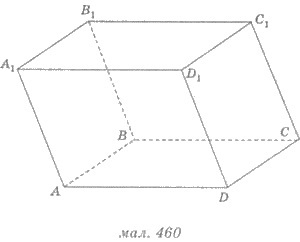
Face a doboz, nincs közös csúcsa, az úgynevezett szemközti oldalon. Ábra 460 szemközti oldallappal vannak arcok ABC D és A 1 B 1 C 1 D 1. AVV1 A1 és C 1 C 1. DD AA 1 D 1 D 1 C BB1 és S.
Tekintsük a tulajdonságok mezőben.
1) párhuzamos szemközti felületei a paralelepipedon és egyenlő.
2) átlói paralelepipedon és a kereszt metszéspont kettéváló.
1. példa Direkt paralelepipedon bázis oldalán 10 cm-es és 17 cm-es, és az egyik átlója a bázis 21 cm-es. A nagy diagonális a paralelepipedon egyenlő 29 cm. Find a terület az oldalsó felületének a paralelepipedon.
Megoldásokat. 1) Legyen a = 10 cm, és b = 17 cm - az alap egyik oldalán; d 1 = 21 cm - átlós alapot. Az ingatlan az átlók a doboz: itt
Mivel 21, a nagyobb átlós a paralelepipedon, amely egy vetülete a bázis sík az átlós a bázis a hossza 21 cm.
. 2) (ábra 459) AC = 21 cm; A 1 P = 29 cm.
3) Mivel a téglatest egy nézete egyenes hasáb, az oldalsó felület S ostor jobb parallelepipedon megtalálható a következő képlettel S = ostor Pl, ahol P - az alap kerületét, l - hossza az oldalsó szélek.
T = 2 (10 + 17) = 54 (cm). S = 54 ostor ∙ 20 = 1080 (cm 2).
2. példa Az alapja egy jobb paralelepipedon a rombusz oldala 4 cm, és hegyesszög 60 °. Minél kisebb a doboz egyenlő az átlós a hosszú átlós a rombusz. Keresse meg a kötet a doboz.
Megoldásokat. 1) Legyen D ABC A1 B1 C1 D 1 - meghatározott állapot paralelepipedon; ABC D - rombusz; AC = 4 cm; B AD = 60 ° (ábra. 461).
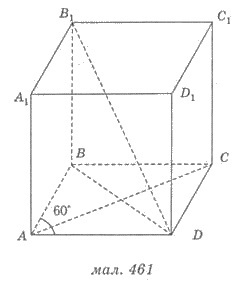
2) egy bázis területet
3) Δ AVB - egyenlő oldalú; AB = BD = 4 cm.
4) Δ ABC: ABC = 90 °. a koszinusz tétel:
5) Mivel az AC D, B 1 D - kisebb átlós a paralelepipedon.