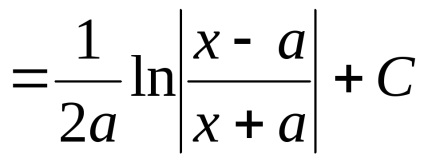Legegyszerűbb integrációs szabályok
I. Bevezetés állandó tényező kívül az integrál jel.
Tétel 3.Postoyanny tényező lehet venni, mint egy jel a határozatlan integrál, azaz
Bizonyítás. Nézzük az származéka a jobb oldali (4.1), és vegye ki az állandó tényező a jele a származék:
.
Használata képletű (2.2). Mivel azt találjuk, hogy
,
azaz, a jobb oldalon a (4.1) egy sor primitívek egy funkciót
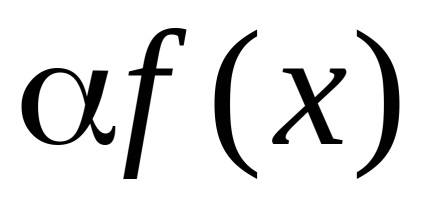
Alkalmazási példák 3. Tétel.
.
II.Predstavlenie integrál összegeként több szempontból.
Tétel 4.Neopredelenny integrál algebrai összege két funkció megegyezik az algebrai összege integrálok ezeket a funkciókat, azaz
Bizonyítás. Csakúgy, mint a tétel bizonyításában 3, mi különbözteti meg a jobb oldalon a (4.2) képletnek. Tekintettel arra, hogy a származék egy algebrai összege egyenlő az algebrai összege származékok, megkapjuk
.
Tehát ahogy kapjuk, hogy
.
Így Tétel 4 bizonyított.
Megjegyzés. Képlet (4.2) kiterjeszthető tetszőleges számú funkciókat. Kiszámításakor a integrálok a jobb oldali (4.2), több tetszőleges állandók. A nagyon értelmében a határozatlan integrál, mint egy sor primitívek az következik, hogy nem szükséges, hogy írjon minden állandók, csak be kell lépnie egy tetszőleges konstans az utolsó kifejezést.
Itt közös alkalmazási példák 3. és 4. Tétel.
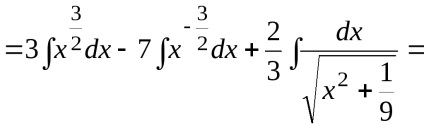
.
.
Az alábbi példák azt mutatják, hogy az integrandus gyakran szükséges, hogy először konvertálni, hogy készítse el a kérelmet a 3. és 4. Tétel.
.
.
.
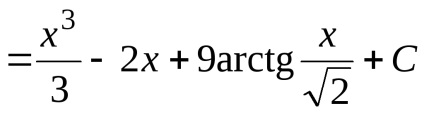
Tétel 5.Pust Ismeretes, hogy
gdeaib- számok
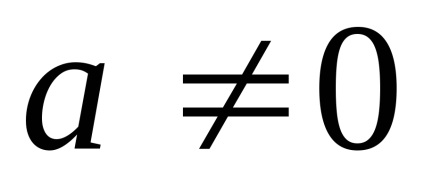
Bizonyítás. Szokás szerint különbséget a jobb oldalon általános képletű (4,3), és azt mutatják, hogy a származék az integrandus függvény a bal oldalon. Megjegyezzük, hogy a funkció
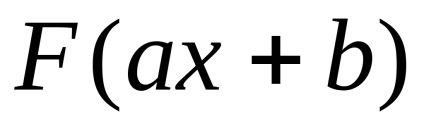
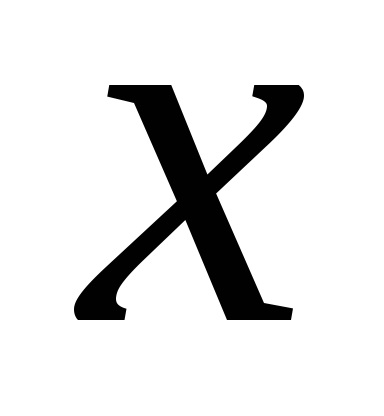
Aztán ott van a lánc egyenlőségek


5. tétel bizonyított.
Vegye figyelembe, hogy olyan (4.3) lehet beszerezni megadásával szerves jele egy új változó
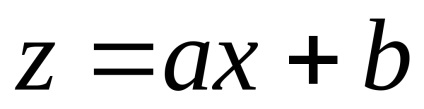
.
kifejező
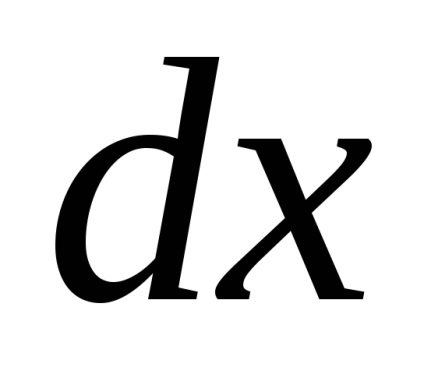
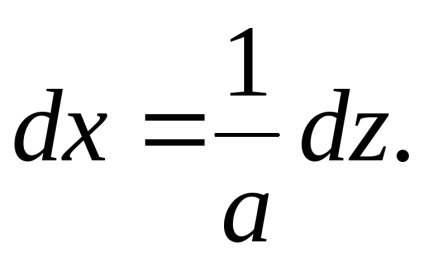
Tehát, meg a lánc egyenletet:
Ez egy lánc (4.4), és kényelmes a használata kiszámításakor konkrét integrálok. Ugyanakkor a bevezetése egy új változó lehet hagyni, ugorjon az utolsó egyenlőség.
Példa 4.10. Bemutatjuk az új változó. majd
4.11 .. Bemutatjuk az új változó. Aztán.
,
A példákban (4,14) és a (4.15) integrandusok korábban képviselt olyan formában, hogy alkalmazni lehet őket integrálok asztalra.
.
Bemutatjuk az új változó. majd
Bemutatjuk az új változó
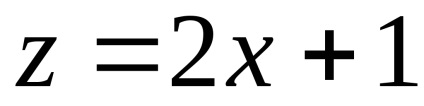
.
Hivatkozva most az 1. táblázatban és levezetni az utolsó előtti három integrál, m. F. (3,13) és a (3,14) és a (3,15) útján 5. tétel.
Számítsuk ki az integrál (3.13) alapján a szerves (3.11) a táblázat.
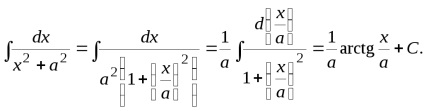
A beépített (3,14) alapján számítjuk ki az integrál (3.12) a táblázat.
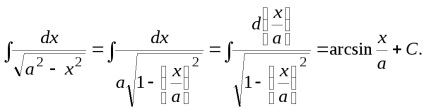
Kiszámításához az integrál (3,15) segítségével táblázatos integrál (3.3).