Lecke „mozgalom
Rövid leírása a dokumentum:
Szöveg kódolása tanulság:
Kezdjük ismerős a fogalom térbeli mozgásától.
A síkrajzi során Ön már ismeri a koncepció a mozgás - ez a térkép a repülőgép, amely megőrzi a két pont közötti távolság.
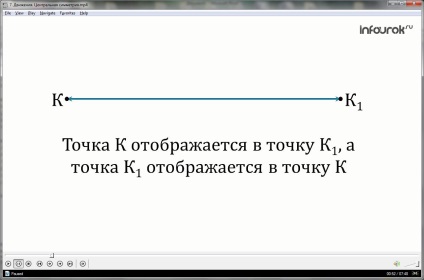
Azt mondják, hogy a leképezés tér önmagára, ha minden egyes pontja a tér rendelt egy bizonyos ponton K1, bármely pontján a tér K1 állították megfelelően bármely pontján K.
Azt mondjuk, hogy egy ilyen kijelző pont K mutatja (mozog) az a pont K1.
Megjegyzendő, hogy egy különleges szerepet játszanak geometria leképezések magára, megőrizve a pontok közötti távolság. Ezek az úgynevezett mozgások helyet.
Így, ha egy pontot a térben, és a mozgás és a B mozgó (jelenik meg), hogy az A1 és a B1, majd AB = A1B1.
Az egyik példa a mozgás központi szimmetria - ez egy feltérképezése saját magára, miáltal bármely pontja K, hogy a pont K1 szimmetrikus ez, viszonyítva a szimmetria középpont B.
1. Legyen a levél közepe körül szimmetria és bevezetni egy derékszögű (négyszögletes) Oxyz koordinátarendszer származási helyén O.
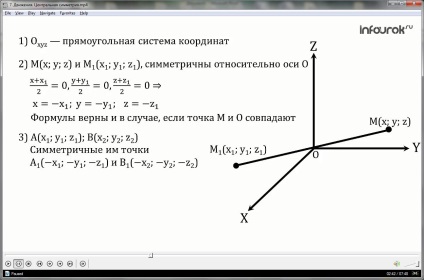
2.Locate közötti kapcsolat pontok M (x; y; z) és az M1 (x1; Y1; Z1), amelyek szimmetrikusak az O ponthoz
Ha M nem esik egybe egy középső szimmetria O, akkor G a középpontját a képletek MM1.Togda felezőpontja koordináták találunk:
x + x1 = 0; y + y1 = 0; z + z1 = 0
Ezek a képletek is érvényesek abban az esetben, ha M és G azonos (magyarázza meg).
3.Rassmotrim bármely két pont: A - koordinátái (x1; Y1; Z1) és B - a koordinátákat (x2; Y2; Z2), és bizonyítja, hogy a pontok közötti távolság az A1 és a B1, hogy azok szimmetrikus, egyenlő AB.
A fenti, már, hogy az A1 és a B1 van koordinátái A1 (-X1; -Y1, -Z1) és B1 (-X 2; -y2; -z2).
A képlet szerint a távolságok két pont között, azt találjuk:
Egyértelmű, hogy AB = A1B1, azaz a pontok közötti távolság mentve.
Így beláttuk, hogy a központi szimmetria a mozgás.
Alkalmazzuk ezt a tudást, hogy megoldja a problémákat.
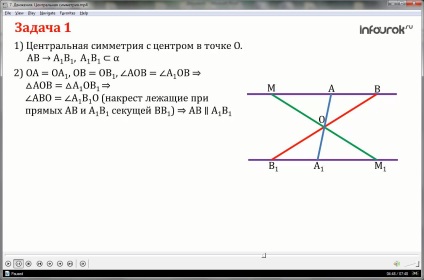
Bizonyítsuk be, hogy a központ a szimmetria egy egyenes vonal nem halad át a középső szimmetria, megjelenik egy vonal párhuzamosan helyezkedik el.
1. Tekintsük a központi szimmetria központ az O pont és egy tetszőleges AB vonal, nem halad át ezen a ponton.
Közvetlen AB és az O pont határozza egyetlen síkban α. A és B pontok jelennek meg a közepén szimmetria a pontban az A1 és B1, amely szintén a síkjában fekszenek α. És ez azt jelenti, hogy az egész vonalon A1 B1 síkjában α.
2. Bizonyítsuk be, hogy az AB egyenes és párhuzamos A1B1.
Mivel a központi szimmetria, akkor OA1 = OA, OB = OB1 szöge egyenlő a szög AOB A1OV1 - függőleges, akkor a háromszög egy háromszög AOB A1OV1 első egyenlőségjel háromszög.
A egyenlőségét háromszögek, ebből következik, hogy a szög ABD megegyezik a szög A1B1, vagyis hazudik keresztben szögek a kereszteződésekben a sorok AB és A1B1 metsző BB1 ezért az egyenesek az AB és A1B1 párhuzamosan.
3. Kimutattuk, hogy jelenik meg a sorban A1B1 központi szimmetria központ O AB. Ehhez az szükséges bizonyítani, hogy egy tetszőleges M az AB vonal mozog egy pontot az M1 és a vonal A1B1 ellentétben tetszőleges pont a vonalon A1B1 bizonyos ponton szimmetrikus vonal AB.
Veszi az AB vonal és bármely pont M, eltér, és húzzuk meg a határt MO. Ez a vonal keresztezi a vonalat A1B1 egy bizonyos ponton az M1.

A szimmetria a központi, majd AB = OA1; MOA szöge egyenlő a szög M1OA1 a függőleges; MAO szöge egyenlő a szög M1A1 mint feküdt keresztben a párhuzamos vonalak AB és A1B1 és metsző BB1. Tehát MAO háromszögek és M1A1 a második egyenlősége alapján háromszögek. A egyenlő háromszögek, ebből következik, hogy a szegmensek a védelmi és OM1 egyenlő, ami azt jelenti, hogy az M pont mozog, hogy a pont M1. A1B1 fekvő vonal szimmetria pont O.
Hasonlóképpen bizonyult beszélgetni bármely pontján M1 szimmetrikus vonalon A1B1 bizonyos ponton M AB egyenes pontja tekintetében O.
Tehát középpontjában szimmetriával vonal nem halad át az O pont, akkor megjelenik egy párhuzamos vonal.
Ma már látható, hogy a leképezés magára, amely megőrzi a két pont közötti távolság, a mozgás, és gondoskodott arról, hogy a mozgási szegmens egyenlő lesz a hossza, egyenes - egyenes vonalban, sík - a síkban. Ennek egyik példája a központi szimmetria.