Lecke - transzformáció expressziós tartalmazó négyzetgyökét extrakciós
Rövid leírása a dokumentum:
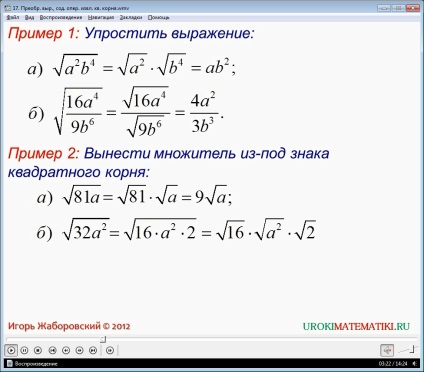
A példák, amelyekben a kívánt konverzió expressziós tartalmazó négyzetgyökét. Ezt jelzi, hogy ezekben a példákban, feltéve, hogy az Au b nem-negatív számok. Az első példában a egyszerűsíteni kell expressziós √16a 4 / 9b és 4 √a 2 b 4. Az első esetben érvényes tulajdonság azt jelzi, hogy a négyzetgyöke a termék a két szám egyenlő a termék a gyökerek őket. Ennek eredményeként a konverziós expressziós kapjuk ab 2. A második kifejezést használják a képlet a négyzetgyöke átalakulás a magán a magán gyökerek. A transzformáció eredményeként a kifejezés 4a 2 / 3b 3.
A második példában kell kivenni a négyzetgyök alatti jel szorzó. Az oldatot kifejezések √81a, √32a 2. √9a 7 b 5. Például négy konverziós kifejezések látható alkalmazott gyökér transzformációs képletű terméket több számok ilyen problémák megoldása. Ebben az esetben, vannak olyan esetek, amikor külön-külön kifejezést tartalmazó numerikus együtthatók, a paramétereket a páros, páratlan mértékben. Ennek eredményeként, a konverziós kapott expresszió √81a = 9√a, √32a 2 = 4a√2, √9a 7 b 5 b 3 = 3a 2 √ab.
A harmadik példa, meg kell végrehajtani egy műveletet, amely ellentétes a korábbi probléma. Talaj tényező a négyzetgyök alatti jel is meg kell tudni használni a vizsgált képletek. Felajánlotta szempontjából 2√2 és 3a√b / √3a hogy a szorzó előtt zárójelben jegyében a gyökér. A jól ismert képlet, az a tényező, az előtte álló gyökér jel, négyzetes és a formába helyezzük egy tényező a munka a gyökér jel. Az első kifejezés megkaphatjuk a kifejezése √8. ló termék formula először alkalmazzák a második kifejezésben lehet átalakítani a számlálót, majd a képlet a saját gyökér -, hogy átalakítsa a teljes kifejezést. A csökkentés után a számláló és a nevező a radicand, kiderül √3ab.
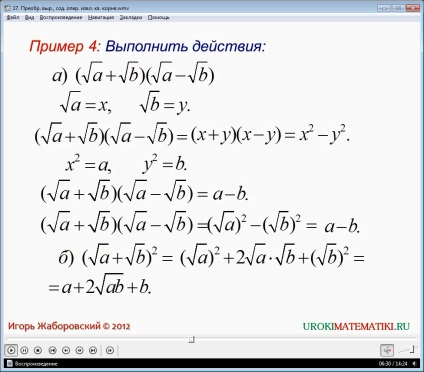
A 4. példában, kell a következő lépéseket a kifejezéseket (√a + √b) (√a-√b). Hogy megoldja ezt a kifejezést vezet be új változókat helyett egytagú a jelet tartalmazó gyökér √a = x és y = √b. behelyettesítése után új változókat nyilvánvaló, hogy képesek a képletek a rövidített szorzás, akkor a kifejezés onnan kapja az x 2 -y 2 Visszatérve az eredeti változók, megkapjuk az a-b. A második expressziós (√a + √b) 2 is alakíthatjuk megszorozzuk Rövidítés Formula. Miután bővülő eredményét megszerezheti a + 2√ab + b.
Az 5. példában, a bomlási végzünk a kifejezések szorzók 4a-4√ab + b + 1 és h√h. végre kell hajtania a konverzió, azokat a közös tényező e probléma megoldásának. Alkalmazása után a négyzetgyök tulajdonságokat megoldások az első expressziós mennyiségét különbség alakul át egy négyzet (2√a-√b) 2. Az oldatok a második expressziós kell rögzíteni a gyökér faktor egy gyökér jel, majd alkalmazza a képletet, hogy az összeg a kocka. Átalakításából származó válik expressziós (√h + 1) (X 2 -√h + 1).
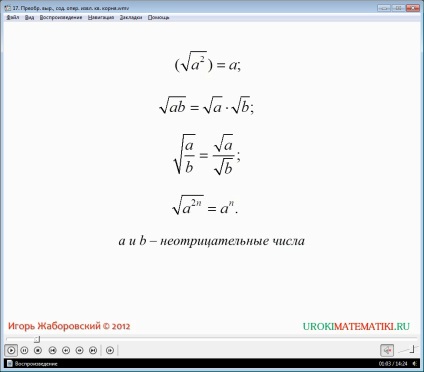
A 6. példában azt a megoldást, ahol az szükséges, hogy egyszerűsítsék egyenlet (a√a + 3√3) (√a-√3) / ((√a-√3) 2 + √3a). beállítás döntést hajtunk végre négy lépésben. Az első lépésben a számláló átalakul egy termék a képlet Rövidítés szorzás - kockák összege két szám. A második felvonásban átalakul nevező, hogy lesz egyfajta-√3a + 3. Átalakítás után lehetővé válik, hogy csökkentsék a frakció. Az utolsó felvonásban is érvényes a képlet a rövidített szorzást, amely elősegíti, hogy a végeredmény 3.
A hetedik például, hogy megszabaduljon a négyzetgyök nevezője frakciók 1 / √2, 1 / (√3-√2). Amikor feladatok megoldására bázikus frakciók tulajdon. Ahhoz, hogy megszabaduljon a gyökér a nevezőben a számlálóban és a nevezőt ugyanazzal a számmal, amellyel a radikális kifejezést négyzeten. Ennek eredményeként a számítások kapunk 1 / √2 = √2 / 2 és 1 / (√3-√2) = √3 + √2.