Lecke - tanulási ütemterv számszerű funkciók
Rövid leírása a dokumentum:
Tartalmaz hasznos, teljes körű és magas színvonalú tájékoztatás, hogy az asszimiláció nem hátráltatja semmi. A diákok könnyen mester az anyag a témában, ahogy felvette szerint számos követelményt, beleértve a hallgatók kor.
Tanítani érthetőbbé teszi az elvet az olvasás grafikonok funkciók, szükséges felidézni, hogy az érvelés hívják, hogy a függő változó és a független változó. Ezt követően felkérte, hogy vizsgálja felül néhány tetszőleges függvény, és szerkesszük meg a grafikont találva számpárok, amelyek a pontok koordinátáinak egy koordináta-rendszerben. Amikor a menetrend épül, bevezette a meghatározása a függvény grafikonján.
A tanulság hasznos lesz mind a tanárok és a diákok számára.
Reading a grafikon egy numerikus funkciót.
A diagramok a funkciók nagy gyakorlati jelentősége van. Különösen a használata funkcionális kapcsolatok és ábrázolási széles körben használják a gazdaságban.
A tanulmány a mai téma, meg kell emlékezni: mi a funkciója az úgynevezett numerikus?
A numerikus függvény egy szabályt, mely szerint minden egyes eleme a készlet X magas társítjuk egyedülálló eleme a beállított y nagy.
Az X az a domain a funkciót.
Állítsa Y hívják a beállított funkció értékeket.
Egyenlőség y értéke X eff hívott függvény egyenlete.
X - független változó vagy funkció érv. y - függő változó.
Az úgynevezett grafikon?
Adott egy függvény y egyenlő az EF x, ahol X tartozik az X-nagy, és megteszi azokat a pár X, Y, és azokat a vonatkozó koordinátasík pont, megkapjuk a grafikonon. Függvény grafikonját - egy grafikon mutatja az összefüggést szett X nagy és y értéke nagy.

Olvassa el a menetrend - ez azt jelenti, hogy át tulajdonságai a funkció,
1) domain a funkció;
2) tartományában az értékeket;
3) függvény nullákat - argumentum értékeket, amelyek a függvény nulla;
4) időközönként állandó jel funkció t.e.promezhutki,
ahol függvényértékeket előjele megegyezik;
5) A intervallumonként monotonitási funkció, azaz intervallumokban, ahol a függvény növekszik vagy csökken;
6) naibolsheei legkisebb a függvény értékét, azaz, A legnagyobb és a legkisebb érték a függő változó;
Tulajdonságok, amelyek nem rendelkeznek az összes funkciók:
9) páros, páratlan;
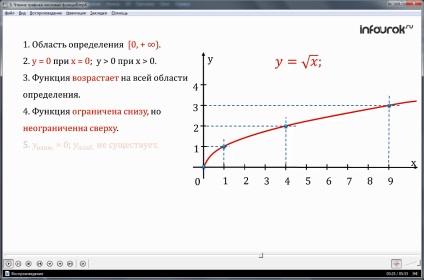
Read grafikonok az ismert funkciók, például, y értéke négyzetgyöke X.
1. mező funkciójának meghatározása -
gerenda nulláról plusz végtelenig
2. Az Y egyenlő nulla X nullával egyenlő; y értéke nagyobb, mint nulla, ha x nagyobb, mint nulla.
3. A funkció növeli a saját domain.
4. A funkció korlátos alulról, de nem határolja felülről.
5igrek legalább nullával egyenlő érhető el X nullával egyenlő; y a legnagyobb van.
6.Funktsiya folyamatos egy adott területen.
7. kör értékek - gerenda nulláról plusz végtelenig
8.Grafik konvexitási felfelé.
y = kx + in

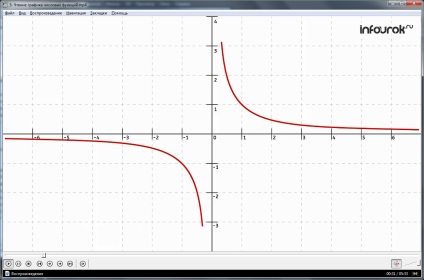
Olvasd grafikon korlátos függvény, amelynek grafikonja ábrázolja
1. terület meghatározása a funkció - intervallum mínusz 3-3.
2.Funktsiya van egy nulla: X jelentése nulla.
3.Polozhitelnye érték függvény, ha x nagyobb, mint nulla és kisebb vagy egyenlő, mint három. negatív - ha x nagyobb vagy egyenlő, mint mínusz három és nullánál kisebb ..
4.Oni növekszik, mivel az első X X vtoroevypolnyaetsya Aeff kisebb egyenlőtlenség X kisebb, mint az első Aeff a második X.
5.Mnozhestvo időközzel értékek mínusz 1-1.
6.Sledovatelno, a legkisebb érték a függvény mínusz egy, a legmagasabb - az egyik.
7.Funktsiya korlátos alulról és felülről.
8.A intervallum mínusz három nullára függvény konvex lefelé, és a
intervallumban nullától háromig felfelé domború.
9.Nepreryvna az egész tartományban.