Lecke - csökkenti a formula
Rövid leírása a dokumentum:
Trigonometry - ez az egyik legfontosabb része, amely tanult során algebra a 10. évfolyamon. Kifizette meglehetősen bőséges mennyiségű tanulságokat. Mert ahhoz, hogy jól megértsük trigonometry mind elméletben, mind gyakorlatban, az kell, hogy folyamatosan megoldani rengeteg példát, amelyek erősítik az elmélet és a készségek növeli a végrehajtás egy munka: otthon, ellenőrzés, önálló, vagy csak jó.
Az anyag, amely bemutatja és vizsgálja az erőforrás által összeállított szakértői úgy, hogy teljesen befedje a témát, ne maradjon le egy fontos pont. Azt mondja, hogy biztonságosan lehet használni a tervek készítése, összefoglalók a tanulságokat, amelyek a fiatal tanárok nélkül nem.
Először tápszerek származnak csökkentése téren. Láthatjuk, milyen egyszerű ez, hogy megszabaduljon a második fokozatot a sinus és cosinus. Ahhoz, hogy a diákok megértsék, ahol nem ezek a képletek, a következő lépés bemondó részletesen leírja az összes lépést. Először is, érdemes megjegyezni az alapvető képlet trigonometrikus, amely azt mondja, hogy az összeg a tér a szinusz és koszinusz ad nekünk egységét. Ez az identitás is megjelenik külön és a tér a szinusz és koszinusz. Emlékezés képlet a sinus és cosinus kettős érv, akkor láthatjuk, hogy hol vannak az új szabályok.
Figyelemre méltó, hogy ha bármelyik lépésben, utalunk az anyagot, amelyet korábban vizsgálták. Ez azt jelzi, hogy fontos és egymással való témák trigonometria. Semmilyen körülmények között nem szabad kihagyni, vagy hogy a témában, és kezdődik egy újat. Anyaga lesz zavaró, mert nem ismert, hogy ha voltak bizonyos értékeket és átalakítás. Mivel trigonometry tartalmaz számos képletek, amelyek nélkül lehetetlen továbblépni, azokat fokozatosan megjegyezni és megtanulni újakat. Szintén rögzíti a szükséges anyag gyakorlatban, valamint új képességek, amelyek hasznosak lesznek később írásakor a teszt és félév munkáját.
Ezt követően, a bemondó kínál megoldani egy hasonló példa, amelyben a általános képletű csökkentésének sine használt. Tanítványai tud oldani önállóan. Ha érteni az előző példában, akkor megbirkózni ezzel.
Az eredmény egy másik összetettebb példáját. Ha a határozat érintője formula használatos. Kiíró határozat részletesen kifejti, majd megjeleníti a választ.
Leengedése a képlet
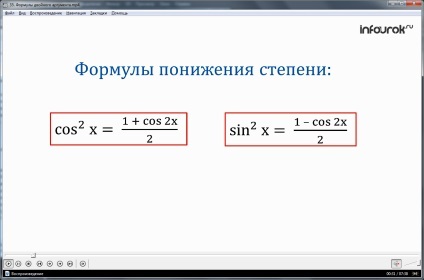
cos 2 x = (x a négyzeten koszinusz egyenlő az összege egységek a félig-dupla és koszinusz argumentum).
= 2 x sin (szinusz-négyzet X jelentése félig különbség egység és a koszinusz kettős argumentum).
nevezik csökkentés mértékét képleteket.
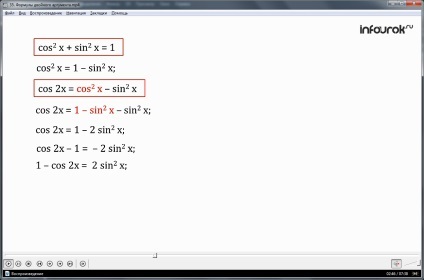
Levezetjük a képletben:
Általános képlet cos 2 x + sin 2 x = 1, 2 x sin lelet:
sin 2 x = 1-cos 2 x
A általános képletű cos 2x cos 2 x = - sin 2 x, 2 x sin értéket helyettesíteni 1- cos 2 x és cos 2 x kapjunk - (1- cos 2 x)
a közzététel zárójelben jutunk cos 2 x - cos 2 x 1 +
mivel cos 2 x + cos 2 x 2 x mennyiségben 2cos
azt találjuk, hogy cos 2x = 2 cos 2 x - 1.
cos 2x = x cos 2 - sin 2 x = cos 2 x - (1-cos 2 x) = 2 cos 2 x - 1.
Ezért kifejezni cos 2 x
cos 2x + 1 = 2 cos 2 x
cos 2 x = (x a négyzeten koszinusz egyenlő az összege egységek a félig-dupla és koszinusz argumentum).
Mi volt az első fokú csökkenése képlet cos 2 x.
Hasonlóképpen, a második és levezetni egy képletet a csökkentés mértékét 2 x sin:
Általános képlet cos 2 x + sin 2 x = 1, 2 x cos találunk:
cos 2 x = 1 - sin 2 x
A általános képletű cos 2x cos 2 x = - sin 2 x, x értéke, cos 2:
helyett 1 - sin 2 x
Kapunk 1 - sin 2 x 2 x sin
Mivel -sin 2 x 2 x -sin összegű így -2 sin 2 x,
Azt kapjuk, hogy cos 2x = 1 -2 sin 2 x.
Ezért kifejezni sin 2 x:
transzfer egységek ellentétes előjelű
cos 2x-1 = -2 sin 2 x
változások jele
1- cos 2x = 2 sin 2 x
osszuk el 2 mindkét oldalon:
= 2 x sin (szinusz-négyzet X jelentése félig különbség egység és a koszinusz kettős argumentum).
Ne feledje, a képlet, hogy mi a továbbiakban a csökkentés mértékét képleteket.
Ezt a nevet annak a ténynek köszönhető, hogy a bal oldalon a két identitás tartalmazza a második a sinus és cosinus és a jobb oldalon - az első fokú, azaz a megfigyelt csökkenése súlyosságát.
Tekintsük a megoldás a példák segítségével a csökkentés mértékét képletek.
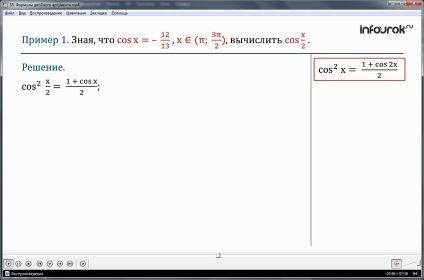
Példa 1. Ismerve, hogy cosx = - és hε (π;) (X tartozik időközzel pi pi három két), kiszámítja cos.
Fogjuk használni a csökkentés mértékét képlet
X négyzetes cosinus cos x = 2, a. kapjuk:
azzal a feltétellel, cosx = - helyettesítjük az adatokat a képlet, van:
cos = 2. a számításokat a jobb oldalon a kifejezés, megkapjuk
cos = 2. kivonat a négyzetgyöke. megkapjuk
A feltétel az π x. ezért. Ez azt jelenti, hogy az az érv X, osztva kettővel tartozik a második negyedévben, ahol a koszinusz negatív. Ezért, a COS = -.
Válasz: cos = -.
2. példa Annak ismeretében, hogy cosx = - és hε (π;)
(X tartozik intervallumban pi pi három két), kiszámítja a bűnt.
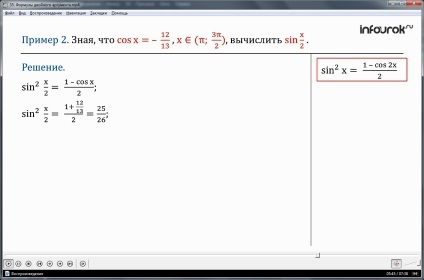
Határozat. Az általunk használt mértékét csökkentő képletű sin 2 x =
2 = sin mert hipotézis cosx = -
Van: sin 2 =. Mi kivonat a négyzetgyöke, és megkapjuk
A feltétel az π x. ezért. Ez azt jelenti, hogy az az érv X, osztva kettővel tartozik a második negyedévben, ahol a szinusz pozitív. Ezért sin =.
3. példa Annak ismeretében, hogy cosx = - és hε (π;) (X tartozik időközzel pi pi három két), kiszámítja tg.
Határozat. Annak ismeretében, hogy az érintő X - X az arány a szinusz a koszinusza X, van
1. és 2. példa, azt találjuk, hogy a bűn = és cos = -. ezért
Válasz: tg = -5.