Lapos és síkgráfok
Planar grafikon - egy grafikon, amely készül a síkban úgy, hogy nincs két széle nem fedik egymást.
Planar graph - grafikon izomorf sík gráf.
Ábra A) - sík, de nem lapos, grafikon b) egy sík gráf.
Mindegyik síkban grafikon osztja a sík szélén: a belső - külső és korlátozott - korlátlan.
A tanulmány a síkgráfok kezdeményezte Euler tanulmányában poliéder. Következő Euler formula - egy klasszikus eredménye a matematika, ahol - a csúcsok száma - élek száma - arcok számát a poliéder. Euler formula csak az általánosabb esetben egy lapos kártya - csatlakoztatott sík grafikon, együttesen az összes aspektusát.
Tétel. Legyen egy síkban kártyának csúcsok, élek és arcok. Aztán ott van a következő egyenletet:
Bizonyítás. Indukciót alkalmazunk a élek számát.
Ha, akkor a képlet (1) a következő alakú :.
Tegyük fel, hogy nincs több (1) általános érvényes minden kártyák számos sík ig. Lapos kártya élek számát nyert lapos kártya az élek számát kétféleképpen:
1) hozzáadásával az új csúcsok, perem, amely összeköti a egyik a régi csúcsok;
2) a vegyület nem egy él két szomszédos csúcsot.
Az első esetben, az (1) képletű ellenőrzik a következőképpen:
.
A második esetben, egy új arc, és a képlet (1) ellenőrzik a következőképpen:
.
Következmény 1. Ha in-kártya által képzett minden arc a gyűrű csúcsok,
Bizonyítás. Az élek száma tartozó mindkét oldalán azonos. Tehát a csúcsok számát kell számítani minden egyes arcot is. Ebben az esetben, minden él kétszer számít, így a csúcsok száma újratervezi. Kapjuk egyenlőséget. Behelyettesítve az (1) és megtalálni (2).
Kuratowski tétel. Graph sík akkor és csak akkor, ha nem tartalmaz részgráf homeomorf vagy.
35. A teljes gráf. Count K4 és K5 sík gráf nem planáris.
Maximális síkbeli gráf egy sík görbe, amely hozzá minden éle már nem sík.
A meghatározás az következik, hogy a maximális síkbeli gráf minden arcok háromszög (metszettel három csúcsok):
ha a vonal tartalmaz egy téglalap (vagy egy sokszög sok oldalán), lehetőség van arra, hogy adjunk egy él, amely nem változtatja meg a síkból a grafikon, de megfosztva a tulajdonságait a grafikon, hogy olyan síkgráfok.
Példa. Az alábbi grafikonon, akkor add csak az egyik él, ami után ez a grafikon készült a grafikonon.
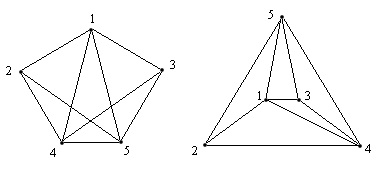
Lemma. Ha - és síkbeli-gráf, akkor
.
Bizonyítás. A legnagyobb számú élek egy sík gráf egy gráf minden arc - háromszög. A maximális síkbeli gráf minden részletét - háromszög. Behelyettesítve (2). Kapjuk.
Tétel. A grafikonok nem planáris.
Bizonyítás. Ha (5.10) -graph sík, akkor a lemma nem teljesül :.
36. páros gráf. Count K2,3 és K3,3 sík gráf nem planáris.
A grafikon az úgynevezett páros gráf. Ha a csúcsok halmaza két nem üres részek (,), amelyen belül nincsenek élei.
Ha az összes csúcsot köti össze minden csúcsának, akkor a gráfnak nevezzük teljes páros gráf, és jelöljük.
Itt látható a teljes páros gráf a csúcsok száma nem nagyobb, mint 4:
Maximális síkbeli páros gráf úgynevezett síkbeli páros gráf, hogy ha minden éle megszűnik planarnymdvudolnym gráf.
Ha - a legnagyobb sík páros gráf minden, az arca egy négyszög:
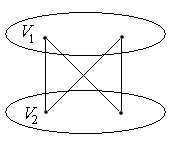
Példa. Az alábbi grafikonon, akkor add csak az egyik él, ami után a grafikon utal, hogy a grafikon:
Lemma. Ha - síkbeli páros gráf, majd -graph a
.
Bizonyítás. A legnagyobb számú élek egy páros gráf egy síkbeli gráf minden arc - quadok. A maximális síkbeli gráf minden részletét - quadok. Behelyettesítve (2). Kapjuk.
Tétel. Grafikonok és nem planáris.
Bizonyítás. Ha (6.9) -graph sík, akkor a lemma nem teljesül :.