Kromatikus száma egy sík gráf
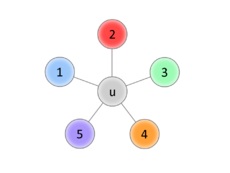
és kapcsolódik hozzá a felső
Elején a bizonyítás ugyanaz, mint az előző tétel a nehézség adódik az indukciós folyosón. Megmutatjuk, hogy a helyzet th színek akkor is vissza a távvezérlő tetején úgy, hogy a színezés maradt helyes.
Jelöljük az - visszaadja a felső - top, színesre festett.
Ha csúcsai között a szomszédos, két csúcs azonos színű, akkor marad legalább egy szabad színe, amely azt fogja festeni.
Ellenkező esetben, tegye a kapott eltávolítása után egy grafikon egy síkon, vissza vertex (amíg színtelen), és száma a színek annak érdekében bejárása szomszédos csúcsok az óramutató járásával megegyező irányba.
Próbáljuk festeni színű. Ahhoz, színezés maradt helyes, átfestés a szomszédos csúcs színét. Ha körében a szomszédos csúcsok csúcsa festeni őket színű, és így tovább. Vegyünk két szokatlan szituációban, amely előfordulhat a feltérképezés során:
- jutunk, hogy egyszer átfestették a felső (és szeretné újra festeni vissza, hogy nem lehet megtenni). Nyilvánvaló, hogy egy ilyen helyzetben lehetetlen, mert mi változott a színe a csúcsa a rendszer, és ha a végén kaptunk egy bypass két szomszédos csúcsot az azonos színű, majd recolors ezen a helyen volt két csúcs azonos színű, és azon a feltételezésen grafikon nélkül volt festve rendesen.
- felérünk, a szomszédos, melyet eredetileg színes, amelyeket nem lehet festeni a (most már van egy szín).
Ha ez a folyamat sikeresen befejeződött, akkor kap rendszeres színezés. Ha átfestésében sikerült szerint a második kiviteli alak azt jelenti, hogy a gráf egy ciklust.
Akkor próbáld ugyanúgy festeni szín, és a mellette levő színes (a későbbi újrafestés). Ha sikerül - színezőanyagok kapunk.
Ha nem, akkor kapott egy újabb ciklust. De sík gráf, akkor két ciklus átfedés mellett a tetején legalább még egy, ami lehetetlen, mert a tetején az első ciklus, és a második - különböző színekben. Tehát ebben az esetben nem áll fenn.