Komplex számok és a képet egy síkban
Komplex számok kapcsán felmerült a feladat megoldása másodfokú egyenlet. Marad a valós számok halmaza, lehetetlen megoldani egy másodfokú egyenlet, amely a diszkrimináns nullánál kisebb.
Komplex számok használnak különböző alkalmazások a matematika. Különösen, az elmélet a komplex funkciók egy erőteljes eszköz a matematikai módszerek a különböző tudományterületeken.
A komplex szám kifejeződése formájában, ahol a valós számok, az imaginárius egység.
Így egy komplex szám bármely rendezett pár valós számok és a valós számok nevezzük abszcisszájának komplex szám valós szám annak ordináta
Bármilyen komplex szám is képviselteti magát egy sík formájában egy pont síkot, amelyen képviselteti komplex számok, az úgynevezett síkját komplex változó
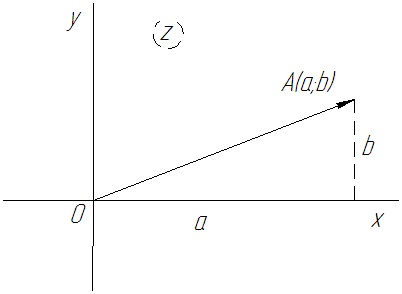
komplex síkban
A valós számok képviselik pont abszcissza képzetes számok képviselik pont ordináta. Ezért tengely az úgynevezett valós tengelye és függőleges tengelyen a képzetes tengelynek.
Csatlakoztatja pont a származás, megkapjuk a vektoros Bizonyos esetekben célszerű figyelembe venni a geometriai vektor kép egy komplex szám Ebben az esetben a valós és képzetes része a vektor az előrejelzések a valós és a képzetes tengelyen.
Jelöljük a poláris koordináták és az origó számolás pólus és a sarki tengely pozitív irányú tengely.
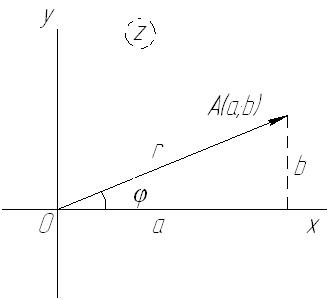
Geometriai kép egy komplex szám
Aztán a következő egyenletek
Ezért egy komplex szám felírható
- ez a trigonometrikus komplex formájában számot nevezzük a modulusa a komplex szám argumentuma komplex szám