kölcsönös tájékoztatás Lecture
CÉL előadások: A koncepció alapján a feltételes entrópia meghatározása kölcsönös információ az ingatlan, és bevezetni a képletet az átlagos összeg a kölcsönös tájékoztatás.
Mérjük az összes rendelkezésre álló mérési és érvényteleníteni mérések állnak rendelkezésre. Galileo Galilei
Az előző fejezetben definiált feltételes entrópia értéke azt jelzi, milyen egy átlagos választás bizonytalanság az egy mennyiség értékének y. Ha az érték x ismert.
Feltételes entrópia teljesíti a következő feltételeket.:
Az üzenetkezelő technológia érdek megszerzésének lehetőségét információra által közvetített üzenetek szimbólumok figyelhető meg a csatorna kimenet. Bemutatott egy matematikai által végrehajtott műveleteket adó és vevő. Az adó és a vevő az úgynevezett diszkrét átalakítók. A konverter bemeneti sorozat a bemeneti jelek egy sáv X, és a kimenet egy kimeneti szimbólum szekvenciát, feltéve ensemble D átalakító lehet egy belső memória. A kimeneti jel ebben az esetben függ nem csak a jelen bemeneti jel, hanem az összes korábbitól. A cél az, hogy meghatározza a szimbólum információt bemeneti x X együttest. tartalmazta a kimeneti jelek az együttes van a kimeneti csatorna, többek között figyelembe véve a meghatározott statisztikai függőség.
Bemutatjuk a jelölést kölcsönös tájékoztatási I (x, y). Összhangban az ingatlan az entrópia 5, tudjuk írni a kapcsolat
Mi szemléltetik grafikusan az entrópia a rendszer és információ
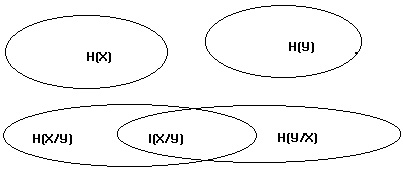
Ábra. 1 Grafikus kijelző kölcsönös tájékoztatás.
Felső ovális elszigetelt - hiányában közötti kommunikáció együttesek változók X és Y;
Alsó kombinációk ovális - ha a statisztikai kapcsolat X és Y között együttesek
Tekintsük sávok X és Y, jellemző a rendszer. Entrópia együttese X ábrázol ovális, amelynek területe H (X): a nagyobb az entrópia, annál nagyobb a területe. Entropy ensemble Y - második ovális, amelynek területe H (Y). Ha a sávok statisztikailag független, azaz nincs kapcsolat közöttük, ovális metszik egymást. Teljes entrópia a rendszer az összege az entrópia, azaz a. E. négyzetösszege.
Ha ez bekövetkezik között együttesek statisztikai összefüggés (korreláció), ovális a diagramon kereszt. A kapott kölcsönös információk I (X, Y) és az a mennyiségi mértékegység e kereszteződés. Entrópia csökken a mennyisége ezt az információt:
Minél nagyobb a kölcsönös információ, a szorosabb kapcsolat, az alsó az entrópia H (X, Y).
Az épület 5 entrópia következik
Összehasonlítva az [5] és [2], azt látjuk, hogy kifejezés [5] jellemzi a kölcsönös egyenlőség az információt az X sávot. ha tudod, hogy a zenekar is. és fordítva, a tudás a ensemble Y, ha X ismert együttest.
Az ingatlan a kölcsönös tájékoztatás.
I (X, Y) ≤ min. Kölcsönös tájékoztatás nem lehet több információt az egyes ensemble egyedül.I (X, Y) ≤ min. A logaritmikus mértéke az egyes sávok külön-külön nagyobb vagy egyenlő, mint a kölcsönös tájékoztatás.
7. A kölcsönös tájékoztatási I (X, Y) van egy maximális (valószínűségi eloszlása egy konvex függvény).
Fejezzük teljes, kölcsönös információt az esélye, hogy a rendszer számára. Ehhez írunk az entrópia értékek az egyes rendszerek a várakozást:
Ezután az expressziós [6] válik
Az expressziós [8] transzformálására matematikai tulajdonságok
elvárások a következők. Egy együttes valószínűségi változók X meghatározhat egy függvény φ (x) minden x értékei. Ez létrehozza a leképezés X sokaságába a valós érték x. együttes
Ez jelenti a értékhatárrendszere halmaza véletlen változók. Kiszámítani a várható értéke y nem kell tudni, hogy a forgalmazás py (y) y valószínűségek. Ha az elosztási px (x) át a együttese X ismert, akkor
Ez a képlet segítségével határozzuk meg, a teljes összeget a kölcsönös tájékoztatás az együttest X a kapott kimeneti csatorna szám az együttes W. kölcsönös információ a bit.
A Markov-forrás modell szerint.
Tekintsünk egy véletlen sorozat bármely események számát. Ha az elemek véletlenszerű sorrendben - valós szám, ezeket a szekvenciákat úgynevezett sztochasztikus folyamatok. elemszám a sorrendben értelmezzük azt az időt, amely ezt az értéket meg. Általában a beállított idő értékek lehetnek folytonos vagy diszkrét halmaza véletlen értékek is lehetnek folytonos vagy diszkrét
ahol p (xi) - előfordulási valószínűsége xi a pillanatban. Ahhoz, hogy ezt a folyamatot elegendő ahhoz, hogy jelezze a valószínűsége p (x) minden x (teljes valószínűségi IHI- 1). Leírni bonyolultabb folyamat modellek alapján kell steady-state tulajdonság, amely lehetővé teszi, hogy egyszerűsítse a matematikai számítások. Az eljárásról azt állítják, hogy helyhez kötött, ha bármely n és t az egyenlet
ahol xi = X1 + t, i = 1, ... N. A sztochasztikus folyamat stacionárius, ha a valószínűsége bármilyen sorrendben nem változik, ha eltolja időben. Numerikus jellemzők, különösen a várakozás stacionárius folyamatok függetlenek időt. Figyelembe véve a steady-state folyamatok, ki tudjuk számítani az idő független az adatok jellemzőit véletlenszerű folyamatok. Példa stacionárius folyamat - olyan folyamat, amelynek értékei függetlenek és azonos eloszlásúak.
Tekintsük további jelet képviselő karakterek sorozata által létrehozott diszkrét forrású üzeneteket.
Shannon határozza diszkrét üzenet forrása: „Feltételezhetjük, hogy a digitális forrás egy üzenetet generál karakterenként. Ő fogja kiválasztani a követő karakterek bizonyos valószínűséggel függően, általában, mint az előző választásokon, és az adott szimbólum. A fizikai rendszer, vagy egy matematikai modell a rendszer, amely létrehozza a szimbólumok sorozatát által meghatározott, megadott valószínűségek, úgynevezett valószínűségi folyamat. Ezért azt feltételezik, hogy a diszkrét forrású képviseli véletlenszerű. Fordítva, bármilyen véletlenszerű folyamat, amely generál egy sorozatot diszkrét szimbólumok választott egy véges halmaz lehet tekinteni, mint egy diszkrét forrás. "
Statisztikai szerkezete a folyamatban, és a statisztikai tulajdonságait a forrás teljesen határozza meg egyváltozós p (i), kétdimenziós p (i, j) a valószínűségek előfordulási elemek üzenete forrás kimeneti. Mint már említettük, ha az egymást követő elemei az üzenet nincs statisztikai összefüggés, a statisztikai szerkezete az üzenet teljesen a kombinációja határozza meg az egydimenziós valószínűsége. A megjelenése egy üzenet elem a forrás kimeneti tekinthető egy adott esemény, amelyre jellemző, hogy a bekövetkezés valószínűsége. Egy sor rendezvények, valamint azok a priori valószínűségek előfordulása van egy koncepció az együttest.
Példák a diszkrét forrás lehet:
Nyomtatott szövegek különböző nyelveken.
Folyamatos források üzenetek digitalizálásukra egy kvantálási eljárást (kvantált beszéd, a televíziós jel.
3. Matematikai esetek, amikor egyszerűen meghatározni elvont néhány véletlenszerű folyamat, amely sorozatot generál szimbólumok.
Ilyen források létrehoz egy sztochasztikus folyamat ismert diszkrét Markov folyamatok. Általában, az eredmény a következőképpen írható le. Van egy véges számú lehetséges „állam” a rendszer: S1, S2.Sn. Továbbá van egy sor átmeneti valószínűségek pi (j), R. E. valószínűsége, hogy egy rendszer állapota Si. akkor megy az állam Sj. Ahhoz, hogy ezt Markov folyamat eredetét egy üzenetet, akkor csak feltételezzük, hogy minden átmenet az egyik állapotból létrehozni egy levelet a másikra. Az állam meg fog felelni a „maradék befolyás” előzi meg a leveleket. A grafikus például „állapot” egy csomóponti ponton az áramkör, és az átmeneti valószínűségek generált, és így a betűket jelzett a megfelelő vonalak.
Egy ilyen forrás a négy A, B, C, B. figyelembe, illetve az átmeneti valószínűségek 0,1; 0,4; 0,3; 0,2, visszatér a csomópont után
ami a következő betű képezhet véges és végtelen sorozata.
Diszkrét forrás lehet hosszabbítani random jel jellemzői, mint a stacioner és ergodicitás. Feltételezve ergodikus forrás lehet „... egyenlővé átlagértékeit néhány szekvencia együtt középértékét együttese lehetséges szekvenciák (a valószínűsége különbség nulla).” Például, a relatív gyakorisága az A betű a privát végtelen sorozatát egy valószın˝uséggel egyenlő lesz a relatív gyakorisága együttest szekvenciák.
A legegyszerűbb forrás generáló modell függő üzenetek egy Markov forrás. Egy véletlen nevezett folyamat lánc Markovasvyaznostis, ha vannak, és minden n x = (x1, ..., xn) ábécé X, a kapcsolatok
Leírás Markov folyamat által adott kezdeti valószínűségi eloszlás szekvenciái értékek az első k és feltételes valószínűségek p (xn / xn-s, ..., xn-1) az összes lehetséges szekvencia. Ha ezek a feltételes valószínűségek nem változott egy műszak alatt szekvenciát ideig homogén Markov-lánc nevezik. A homogén Markov-lánc kapcsolódik s = 1 nevezzük egy egyszerű Markov-lánc. Leírni, elegendő, hogy jelezze a valószínűségi eloszlás p (x1) x tartozó X halmaz és a feltételes valószínűségek
az úgynevezett átmeneti valószínűségek a Markov-lánc.
Az átmeneti valószínűségek kényelmesen írva a formájában egy négyzetes mátrix a M- M méretű
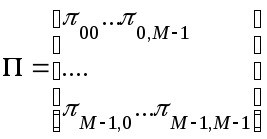
az úgynevezett átmeneti valószínűség mátrixban. Ez a mátrix - sztochasztikus (nem-negatív, az elemek az egyes sorok egyenlő 1).
vagy mátrix formában
Egy tetszőleges számú lépésben, kapjuk az N
,
t. e. az átmenet valószínűsége a n lépésben lehet kiszámítani, mint a mátrix elemeinek. Tegyük fel, hogy van egy sztochasztikus vektor kielégíti a következő egyenletet
Sztochasztikus p vektor, kielégíti a következő egyenletet [2], az úgynevezett a stacionárius eloszlása a Markov-lánc átmeneti mátrix által meghatározott Π. A végső valószínűségi eloszlás a vektor
P∞ mérete független a kezdeti eloszlása a t idő. E. A stacionárius eloszlása. Láncok, egyenlettel meghatározott [3], az úgynevezett ergodikus. Ha az összes mátrix elemeinek Π pozitív és nem nulla, a megfelelő ergodikus Markov-lánc. Annak érdekében, hogy fogalmazza meg a szükséges és elégséges feltétele a ergodicitást mutatunk be néhány definíciót.
Continuity idostizhimo a j állapot, ha valamilyen N a valószínűsége átmenet i állapot, hogy j állapot N lépésben pozitív. Az állapotok halmaza nevezzük zárt. Ha nincs állam C nem lehet elérni az állam a bejövő C.
A lánc az úgynevezett irreducibilis. ha nincs zárt halmazok mellett a készlet minden államban. A Markov-lánc irreducibilis akkor és csak akkor az állam elérhető egymástól. I állapot nevezzük periodikus, ha létezik t> 1: hogy a valószínűsége átmenet i i n lépéseket egyenlő nullával minden n nem többszöröse t. A lánc, amely nem tartalmaz periodikus Államokban az aperiodikus. Periodikus redukálhatatlan ergodikus Markov-lánc.
1. C. Shannon, működik információelmélet és a kibernetika. M. Ed. "IL" 1963 249. oldal -. 259.