Kiszámítása maximális és minimális a célfüggvény a grafikus-analitikai módszer
Az értékek az index sorok nem-negatív, így megkapjuk az optimális megoldás:,; .
Válasz: A maximális eredmény eladásából származó iparcikk, egyenlő 160/3 egység. Ez biztosítja a kiadás csak a második típusú termékek mennyiségének 80/9 egység.
Cél № 2
Dana nemlineáris programozási feladat. Keresse meg a maximális és minimális a célfüggvény a grafikus elemzési módszer. Készítsen Lagrange-függvény és azt mutatják, hogy elégséges feltételei a minimum (maximum) fut a szélsőérték pont.
mert az utolsó számjegy a kódszám 8, akkor A = 2; B = 5.
mert utolsó előtti számjegyű kódszám 1, akkor válassza ki a feladatot az 1. számú.
1) Rajzolj egy régiót, amely meghatározza a rendszer egyenlőtlenségeket.
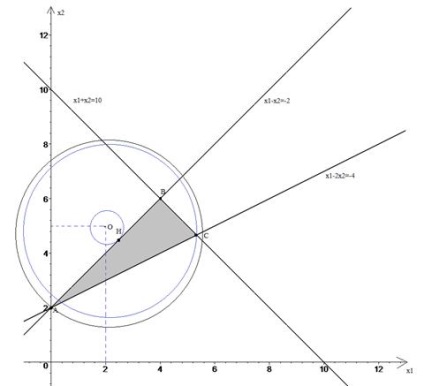
Ez a terület - a ABC háromszög csúcsa koordinátái: A (0, 2); A (4, 6) és a C (16/3; 14/3).
A szintek a célfüggvény a köröket center pontban (2; 5). A négyzetek sugarak lesz az értékeket a célfüggvényt. Aztán ábra azt mutatja, hogy a minimális érték a célfüggvény kapunk pontban H, a maximális - vagy pont vagy a C. pontban
Az érték a célfüggvény a ponton k;
Az érték a célfüggvény a C pontban :;
Ennélfogva, a legnagyobb értéket elérték a pont (0, 2), és egyenlő a 13.
Megtaláljuk a pont koordinátáit N.
Ehhez figyelembe vesszük a rendszer:
Line kör érintője, ha az egyenletnek egy egyedülálló megoldás. A másodfokú egyenlet van egy egyedi megoldás, ha a diszkrimináns 0.
Aztán; ; - a legkisebb érték a funkciót.
2) a Lagrange-függvény a megállapítás a minimális megoldást:
Elégséges feltételei extrémuma:
A rendszernek van egy megoldás, azaz, Elégséges optimalitási feltételek teljesülnek.
A Lagrange-függvény számára megtalálni a maximális felbontás:
Elégséges feltételei extrémuma:
A rendszer tartalmaz egy olyan megoldás, hogy van, Elégséges optimalitási feltételek teljesülnek.
Válasz: A minimális cél úgy érhetjük el; ; legfeljebb az objektív függvény érhető el, ha; .
Cél № 3
Két vállalkozás mennyiségben pénzeszközök d egység. Elosztása során az első entitás jelent évente x egységet biztosít jövedelmet K1X egységek elosztását és a második vállalkozás y egység azt jelenti, hogy jövedelmet biztosít k1y egység. Az egyensúly a az év végén az első vállalkozás nx. egy második én. Hogyan osztja ki a forrásokat a 4 év alatt a teljes bevétel volt a legnagyobb? Probléma megoldva módszerével dinamikus programozás.
Az egész időtartamára 4 éves osztott 4 fázisra, amelyek mindegyike egyenlő egy év. Nézzük felsorolni azokat a szakaszokat, az első évben. Hagyja, Xk és Yk - alapokat, illetve a vállalkozások A és B k - ebben a szakaszban. Akkor az összeg a HK + Yk = ak teljes mennyisége a felhasznált források a k - a színpad és a fennmaradó az előző fokozat K - 1 az első szakaszban segítségével az összes elkülönített források és a1 = 2200 egység. jövedelem érkezik a k - a színpad a kiosztási Xk és Yk egység lesz 6Hk + 1Yk. hagyja, hogy a maximális jövedelem az utolsó szakaszában kezdve k - a színpad fk (ak) egység. mi írjuk a funkcionális Bellman egyenlet, amely kifejezi azt az elvet az optimum: mi lett volna az eredeti állapot és a kezdeti döntés a későbbi határozat legyen optimális a az állam az induló állapot:
Minden egyes szakaszban, akkor ki kell választania Hk. és AK- érték Yk = Xk. Ezt szem előtt tartva, azt látjuk, a megtérülés k - a színpadon:
Funkcionális Bellman egyenlet fog kinézni:
Tekintsük az összes lépést, kezdve az utolsóig.
(Mivel a maximális lineáris függvény érhető végén a [0, a4] ha X4 = a4);
(Mivel a maximális lineáris függvény érhető végén az intervallum [0; a3] X3 = a3)
(Mivel a maximális lineáris függvény érhető végén a [0, A2] az x2 = a2)
(Mivel a maximális lineáris függvény érhető végén az intervallum [0; a1] X1 = a1). a1 = y1 - X1 = 0.
Így a maximális jövedelem a 4. év lesz
V: A pénzt kell fektetni csak a társaság és a teljes bevételt az évben eléri a 16,473.6 4 db.
Feladat száma 4
Határozzuk meg - optimális parametrikus skáláját termékek megfeleljenek az előre meghatározott kereslet, azaz a számát típusú termékek N, a paraméterértékek (k = 1,2, ..., 5) a termékek, amelyek esetében a teljes költség alacsony, sok fajta termék, minden egyes termék által kiszolgált a kiválasztott K-st típus - a tételek számát minden típusú támasztott kereslet kielégítéséhez szükséges, és a legkisebb költség minden egyes termék K-edik típusú:
Építeni egy teljes döntési fa és megmutatni, hogyan ágai alkalmazásával vágják elágazás és korlátozás módszere, és ennek következtében csökkenti a számítások képest az eljárás teljes