Kiszámítása mátrix determináns

Bevezetésének szükségességét meghatározó - száma jellemző négyzetes mátrix, -tesno kapcsolatos oldat lineáris egyenletek. Meghatározója egy jelöljük | A |

A meghatározó a mátrix az elsőrendű A = a11. vagy meghatározója az elsőrendű, az úgynevezett A11 elem. Δ1 = | A | = a11

Tegyük fel például, A = (3), majd a Δ1 = | A | = 3

A meghatározója a mátrix másodrendű A = (aij), vagy egy meghatározója a másodrendű, az a szám, amelyet alábbi képlettel számítottuk ki:

Determináns harmadrendű mátrix A = (aij), vagy a harmadik rend, az a szám, amely képlettel számítottuk ki:

A számítás a meghatározója a harmadrendű eljárás Sarryusa használatra. Írunk le az összes elem a meghatározó és attribútum jobb az első két oszlop a meghatározó:

Vegyük a „+” jel a termék az elemek a fő diagonális és annak két párhuzamos vonal (azaz, hogy a jel a termék megváltoztatása nélkül), és a „-” jel terméke a másodlagos átlós elemek és két párhuzamos egyenesek rá (például, jele a termék elemek fordítva). Figyelembe algebrai összegét, megkapjuk a meghatározója a harmadik rend.

Probléma 1. Számítsuk ki a meghatározója a harmadik rend:

tulajdonságai determinánsok

1. Interchange a két oszlop vagy két sor determináns egyenértékű megszorozva -1.
2. Ha a determináns két azonos oszlopok vagy két sorban azonos, egyenlő nullával.
3. A szorzás összes eleme egyetlen oszlopban vagy sorban a determináns akárhány lambda egyenértékű megszorozzuk a determinánst ezt a számot λ.
4. Ha minden eleme egy oszlop vagy sor determináns nulla, akkor a determináns értéke nulla is.
5. ez nem változik, ha a meghatározója a mátrix átültetés, azaz | .. A | = | A T |
6. Ha az elemek a két oszlop vagy két sorban meghatározó arányos, a determináns nulla.
7. Ha az elemek egy oszlop (sor) a meghatározó adjuk hozzá a megfelelő elemeket egy másik oszlop (vonal) szorozva minden közös tényező lambda, az értéke a meghatározó nem változik.

Következő meghatározó tulajdon kapcsolatos fogalmak és algebrai kisebb kiegészítésekkel. Kisebb M ij eleme egy ij A mátrix A = (A ij) (i, j = 1,2, ..., n) n-edik rendű nevezzük determinánsa (n-1) -edik érdekében, a kapott mátrix a törlést az i-edik sor és j-edik oszlop. Például egy kis része 32 a harmadik rend az a meghatározó a mátrix második sorrendben:

A kofaktor Aij eleme aij A mátrix n-ed rendű nevezzük annak csekély venni a jel (-1) 1+ j.

8. (Laplace tétel) meghatározó az összege a termékek elemeinek bármely oszlop (sor) által kofaktorok, azaz ha A = (aij), akkor:

(Felbontása elemek i-edik sorának; i = 1,2,3, ..., n);

(Bomlik az elemek az oszlop j-dik; J = 1,2, ..., n.).

Probléma 2. Számítsuk ki a meghatározója a mátrix:

Válasszon egy oszlopot (vagy sor) tartalmazó legtöbb nullák, például az első sorban, és bontsa ki a meghatározó a property determinánst 8. kapjunk harmadrendű. is láthatjuk, hogy a 8-bomlás tulajdonság, mint például a harmadik oszlop:

A ychislenie mátrix determinánsa MS Excel

Kiszámításához a meghatározója a mátrix formában a lap MS Excel táblázatkezelő:

• Mi határozza meg a kezdeti mátrixban.
• Mi határozza meg a helyét az eredmény.
• Utalva a mester funkciókat találunk a funkció MDETERM. végre megfogalmazása a probléma.

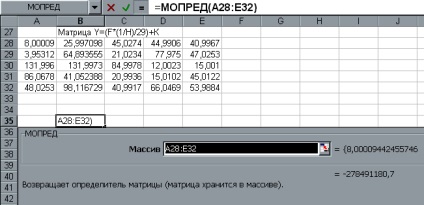
Hogy teljes legyen a munka közben a Shift / Ctrl / Enter

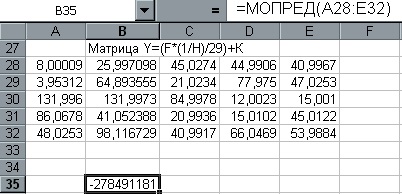
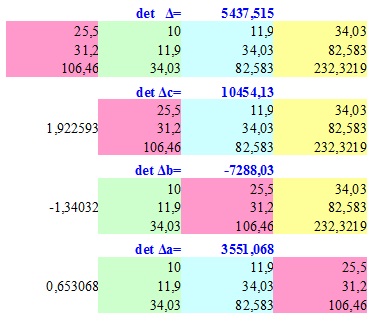
A számítási eljárást a meghatározója a mátrix rendszer A fenti egyenletek egy adott példája egy parabola másodrendű legkisebb négyzetek módszerével, lásd

A számítás a meghatározója a mátrix transzponáltja lásd p.V szezonális kiigazítása az idő sorozat

Lásd még a témával kapcsolatban: