Kirchhoff törvénye - a képlet, példákkal illusztrálva
Kirchhoff törvények létrehozása közötti kapcsolatok áramok és feszültségek az elágazó áramkörök tetszőleges típusú. Kirchhoff törvények különösen fontos villamosmérnöki miatt a sokoldalúság, a megfelelő megoldani minden elektromos problémákat.
Az első Kirchhoff törvénye következik a törvény megőrzése díjat. Ez abban áll, hogy az algebrai összege áramok minden konvergens csomópont nulla.
ahol - a száma áramok, hogy konvergál a csomóponttal. Például, egy elektromos áramkör szerelvény (. 1. ábra), az egyenlet az első Kirchhoff törvény felírható I1 - I2 + I3 - I4 + I5 = 0
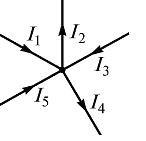
Ebben az egyenletben, az áramokat irányítani a csomópont vett pozitív.
Kirchhoff második törvénye: algebrai összege a feszültség kiválasztott helyeibe Zárt hurkú önkényesen kiválasztott komplex elágazó láncú, egyenlő az algebrai összege a feszültség ebben az áramkörben
ahol k - száma EMF források; m - az elágazások száma egy zárt hurokban; Ii. Ri - ellenállás és áram I th ága.
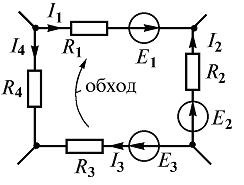
Tehát, egy zárt hurok áramkör (2. ábra). E1 - E2 + E3 = I1R1 - I2R2 + I3R3 - I4R4
Megjegyzés a jelei a kapott egyenlet:
1) EMF pozitív, ha az iránya egybeesik az irányba önkényesen kiválasztott megkerülő áramkör;
2) a feszültségesést az ellenálláson pozitív, ha az iránya a benne egybeesik az irányt bejárás.
Kiszámítása elágazó áramkör segítségével Kirchhoff törvények
A módszer lényege összeállítása egyenletek az első és második törvényei Kirchhoff a csomópontok és kontúr áramkör és megoldani ezeket egyenletek meghatározzuk az ismeretlen áramlatok ágak és rájuk - feszültségek. Ezért az ismeretlenek száma megegyezik a fiókok száma b. Ezért az azonos számú független egyenletet kell tenni, az első és második törvényei Kirchhoff.
A számú egyenlet, amely származhat az első törvény egyenlő a számát áramköri csomópontok, és csak a (y - 1) egyenletek függetlenek egymástól.
egyenletek függetlenség biztosított kiválasztásával csomópontokat. A csomópontok általában úgy választjuk meg, hogy az egymást követő csomópont eltér a szomszédos csomópontok legalább egy ága. A fennmaradó egyenletek által készített második törvénye Kirchhoff a független áramkörök, azaz száma egyenletek b - (y - 1) = b - y +1.
Contour nevezzük független, ha legalább az egyik ágon, amelyek nem tartoznak más áramköröket.
Kirchhoff képezik az egyenletek az áramkör (3.). Az áramkör tartalmaz négy csomópont és a hat ág.
Ezért, szerint az első törvénye Kirchhoff össze y - 1 = 4 - 1 = 3 egyenletet, és a második b - y + 1 = 6 - 4 + 1 = 3. Ugyancsak a három egyenletet.
Tetszőlegesen válasszon egy pozitív áram iránya az ágak (4.). áramkörök kitérő irányba döntünk az óramutató járásával megegyező irányban.
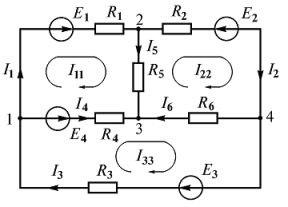
Azt, hogy ki a szükséges számú egyenletek az első és második törvényei Kirchhoff
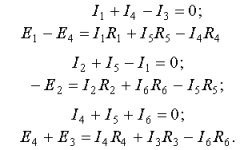
A kapott egyenletrendszert megoldódott áramok. Ha a számítás az áram a ág fordult mínusz, akkor annak iránya ellentétes irányban elfogadott.
Kirchhoff törvények komplex formában
Mert áramkörök szinuszgörbétől Kirchhoff törvények megfogalmazása ugyanúgy, mint az egyenáramú áramkörben, de csak a komplex értékek az árammal és feszültséggel.
Az első törvénye Kirchhoff. „Algebrai összege az aktuális csomópont komplexek az áramkör nulla”
A második törvénye Kirchhoff. „Mindenesetre zárt áramkör integrált algebrai összege egyenlő elektromotoros algebrai összege a komplex feszültség egyáltalán passzív elemei ennek a körnek.”