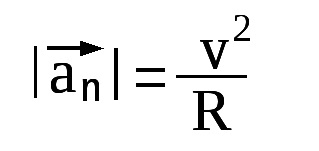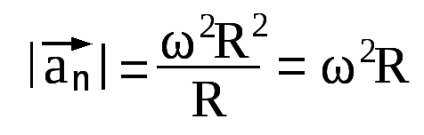Kinematikája forgómozgást

A szögsebességvektorára a forgatási szöget, a szöggyorsulás

Kommunikációs lineáris és szögsebesség

Kommunikációs egyenes és sarkos jellemzők

1. A tangenciális és normális gyorsítás

Két gyorsuláskomponensek: tangenciális gyorsulás és a normál gyorsulás.

Tangenciális gyorsulás mentén irányul érintő a röppálya

Normál gyorsulás mentén irányul normális a röppálya

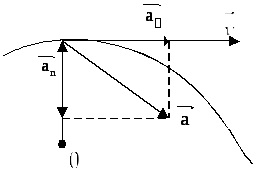
Tangenciális gyorsulás jellemzi a gyors változás értékét. Ha a sebesség nem változik a nagysága, a tangenciális komponens nullával egyenlő, és a rendes összetevője gyorsulás teljes gyorsulás.

Normál gyorsulás jellemzi a gyors változás irányát. Ha az irányt a sebesség nem változik, a mozgás bekövetkezik mentén egyenes pályára.

Általában a teljes gyorsulás:

Így a szokásos komponense gyorsulásvektor

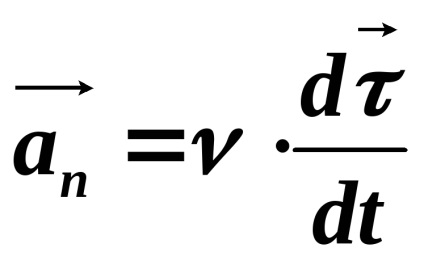
Ahhoz, hogy megtudja, a tulajdonságait a normál gyorsulás, azt kell megállapítani, mi határozza meg,

, azaz a változás mértéke az idő múlásával, az irányt a pálya érintője. Ő a nagyobb (), A több ívelt pályája, és a gyorsabb a részecske mozog egy útvonal mentén.

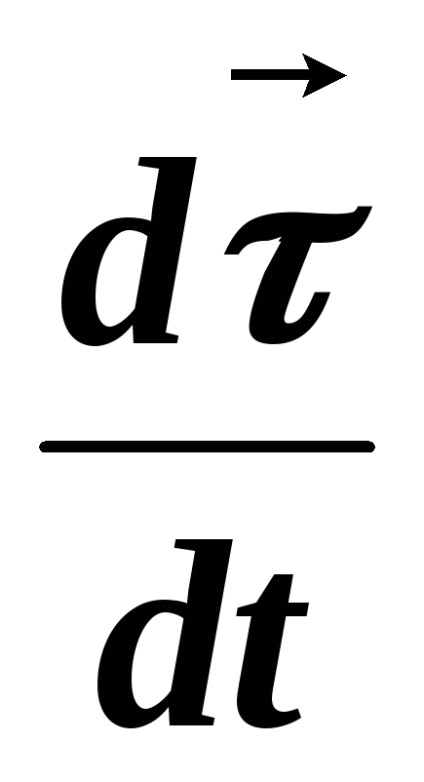
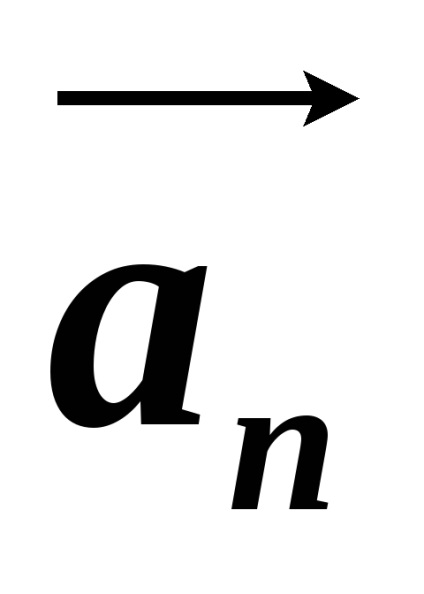
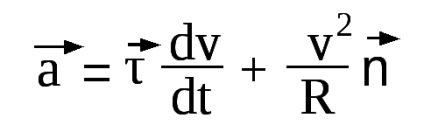
2. A görbületi sugár a pálya

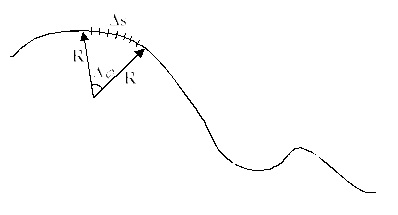
A görbületi sugár - a kör sugarát, amely egyesíti az e helyen infinitezimális része annak görbe.

3. A szögsebességvektorára az elforgatás szögét a szöggyorsulással.

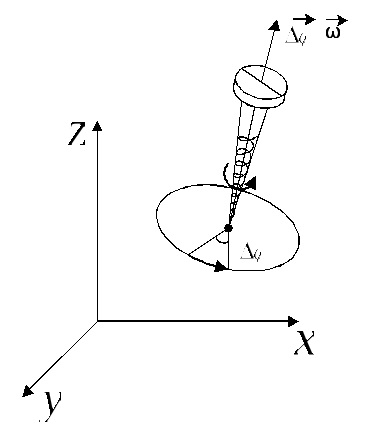
Bármilyen forgása teljesen határozza megadásával a forgástengely és a szög povorotaΔφotnositelno ezen a tengelyen. Ha a forgatás végezzük egy kis ugolΔφ <<2π, то можно ввести понятие вектор угла поворота.

vektor

irányította a forgási tengely mentén, azaz merőleges a síkra, amelyben a forgás bekövetkezik.

A tájékozódás ezen vektor határozza meg a jobbkéz-szabályt.

Az abszolút értéke a vektor

povorotaΔφ ugyanabban a kanyarban.

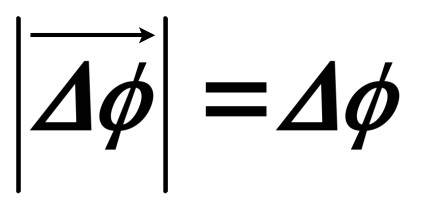
Ahhoz, hogy értékeljük vektort, akkor nem csak az irányt, és abszolút érték, hanem, hogy megfelel a jogállamiság vektor összeadás. Belátható, hogy a vektor kívül két elfordulási szög a paralelogramma nem hajtjuk végre. Ez csak akkor érvényes, az malogoΔφ <<2π

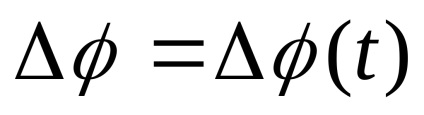
Szögsebesség vektor

, irányt, amely meghatározza a tájékozódás a forgási síkjával jobbkéz-szabályt, és a forgásirányt.

vektor hossza

Ez a származék a forgatási szög idővel:

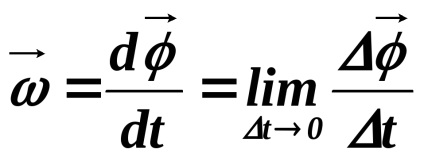
Szögsebesség, ellentétben a forgatás szögét, a teljes vektor.

vektor

változhat, mint a változó a forgási sebességét a test egy tengely körül (legnagyobb), és a forgatás miatt forgástengely egy olyan térben (irány).

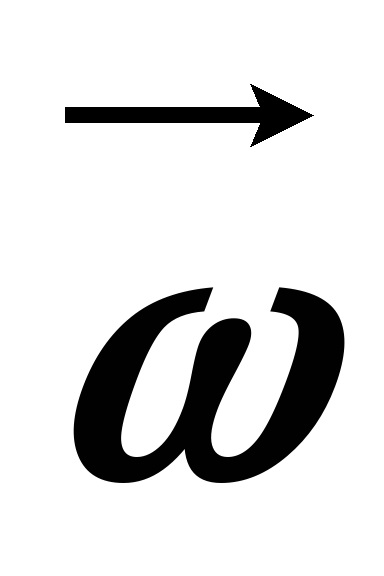
Az időbeli változását a szögsebesség jellemzi a szöggyorsulás:

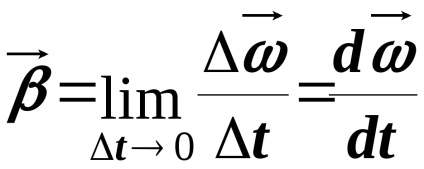
szöggyorsulás modul mérik

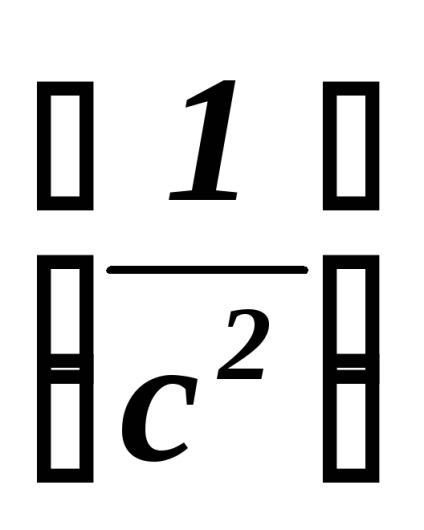
Szöggyorsulással valamint a szögsebesség - ál.

- pseudovec- mert a forgásirányt a vektor társított a szervezet forgásirányt.

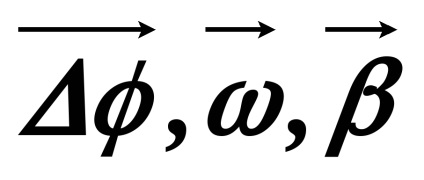
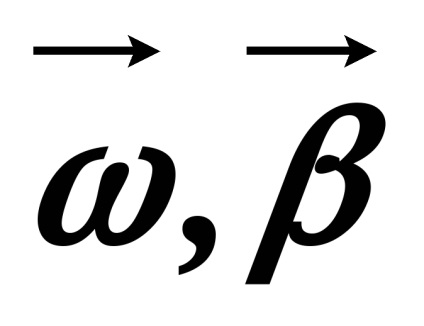
4. Kommunikáció lineáris és szögsebesség

Hagyja a malyyΔttelo fordult naΔφ. Hagyja, hogy a pontokat a

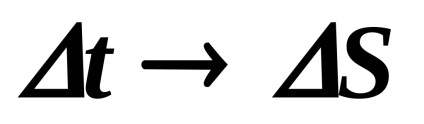
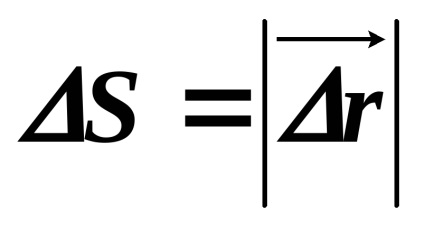
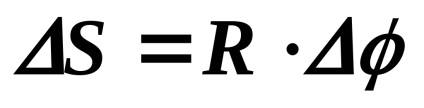
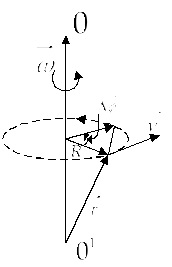
lineáris sebesség modul

Kommunikációs vektorok lineáris és szögsebessége: a pont pozícióját határozza meg a sugár vektor

, vektoraz ábrán úgy definiáljuk, mint a vektor termékés.

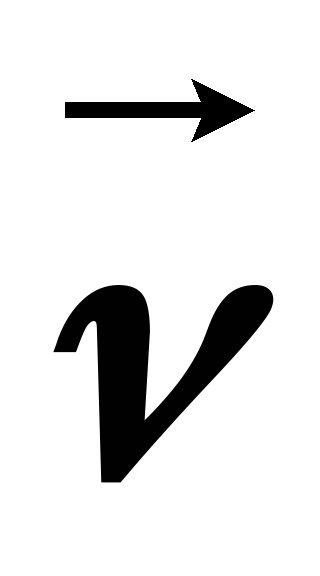
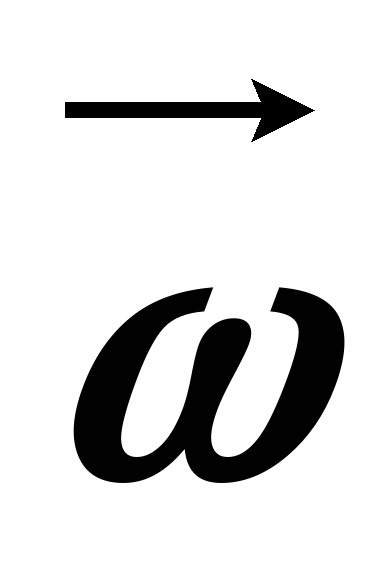
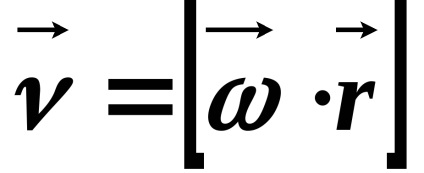
A változás a sugár vektor

végül csak az irányt nevezzük precesszió.

5. Kommunikáció egyenes és sarkos jellemzők

Kapcsolódó cikkek

• A forgó mozgás egy rögzített tengely