Kidolgozása egy matematikai modell, az időbeli és frekvencia karakterisztika egy adott elem
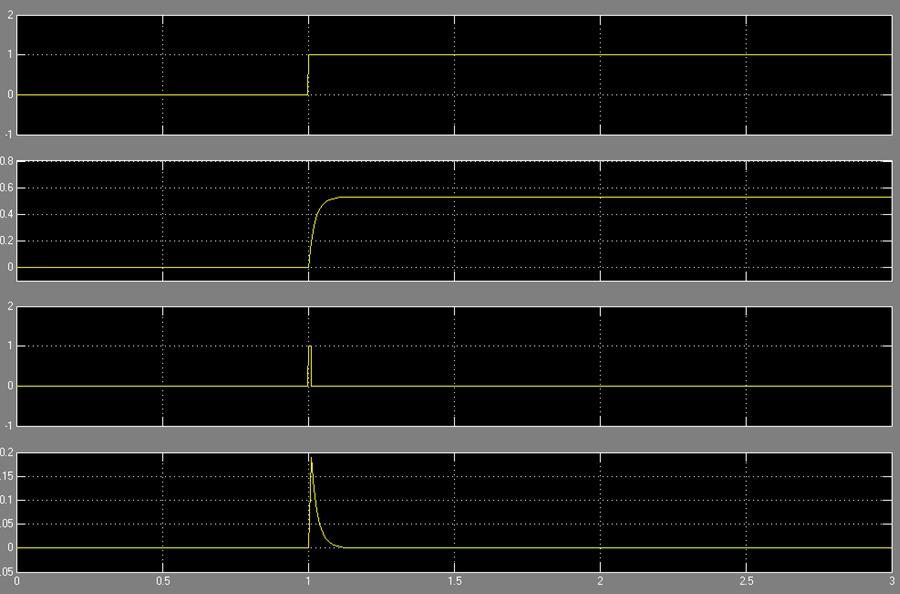
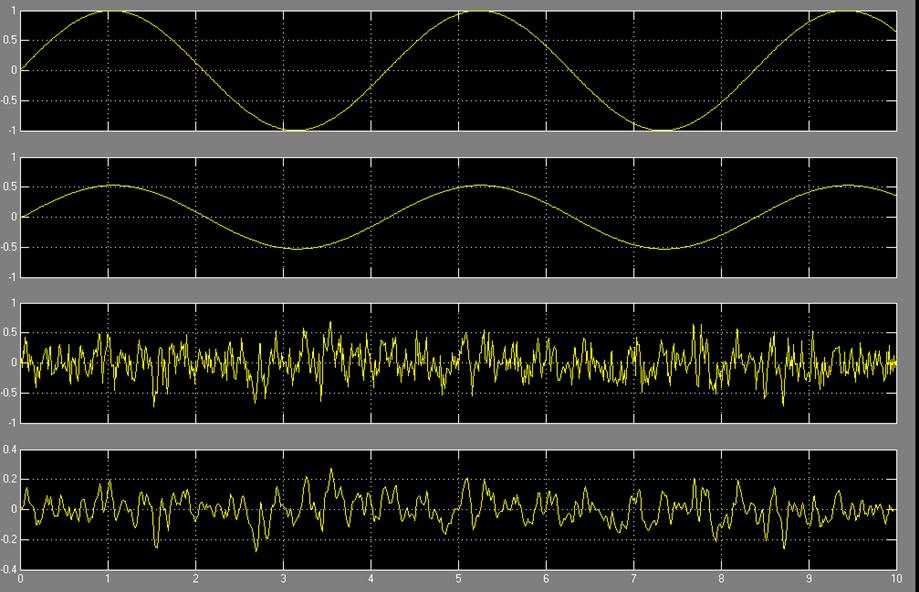
A 4. ábra „ütemterve az átmeneti folyamatot és a súlya a rendszer funkció”
Mint látható a grafikonon, az értékeket találtunk a súlyt és átmeneti jellemzői igazak.
1.5. Mi kiszámítjuk és telek amplitúdó és fázis
frekvencia jellemzői logaritmikus frekvencia
sejtkarakterisztikáiból. Mi ellenőrzi vMathCad.
Sequence találni frekvencia jellemzői:
- hogy a változás az átviteli függvény p = j · ω
- megszabadulni képzetes számok a nevezőben
- nyissa meg a konzolok és az eredmény hasonló kifejezések, és megosztani a számlálóban az összeg a valós és képzeletbeli polinomok
- írjon egy kifejezés a valós és a képzetes polinomok
- írjon egy kifejezés a logaritmikus frekvencia átvitel
- konstrukció grafikonok frekvencia jellemzőit.
ahol U (ω) - a tényleges frekvencia
V (ω) - gyakorisága jellemző a képzeletbeli
Mi helyettesíti az együtthatók:
Készítünk egy frekvencia válasz:
5. ábra „Graph amplitúdó-frekvencia jelleggörbe”
Készítünk amplitúdó-fázis jellemző (poláros plot):
Mi megépíteni a fázis válasz:
Fig.7 „Graph fázis válasz”
Készítünk egy logaritmikus frekvencia átvitel:
8. ábra „ütemezése logaritmikus amplitúdó-frekvencia karakterisztika”
Ellenőrizze a helyes frekvencia jellemzőit számítási eszköz segítségével MathCAD.
Írunk a kifejezés az építési frekvencia karakterisztika segítségével beépített funkciókat MathCAD.
A1 (w) - az amplitúdó-frekvencia jelleggörbe
Fig.11 „ütemezése logaritmikus amplitúdó-frekvencia karakterisztika”
Az ellenőrzés azt mutatta, hogy a frekvencia karakterisztika a vezérlő objektum épített helyesen.
1.6. A Matlab alkotják az áramköri szimuláció és proizvedom halad át a vizsgálati elem lépésenként. impulzus és szinuszos jel.
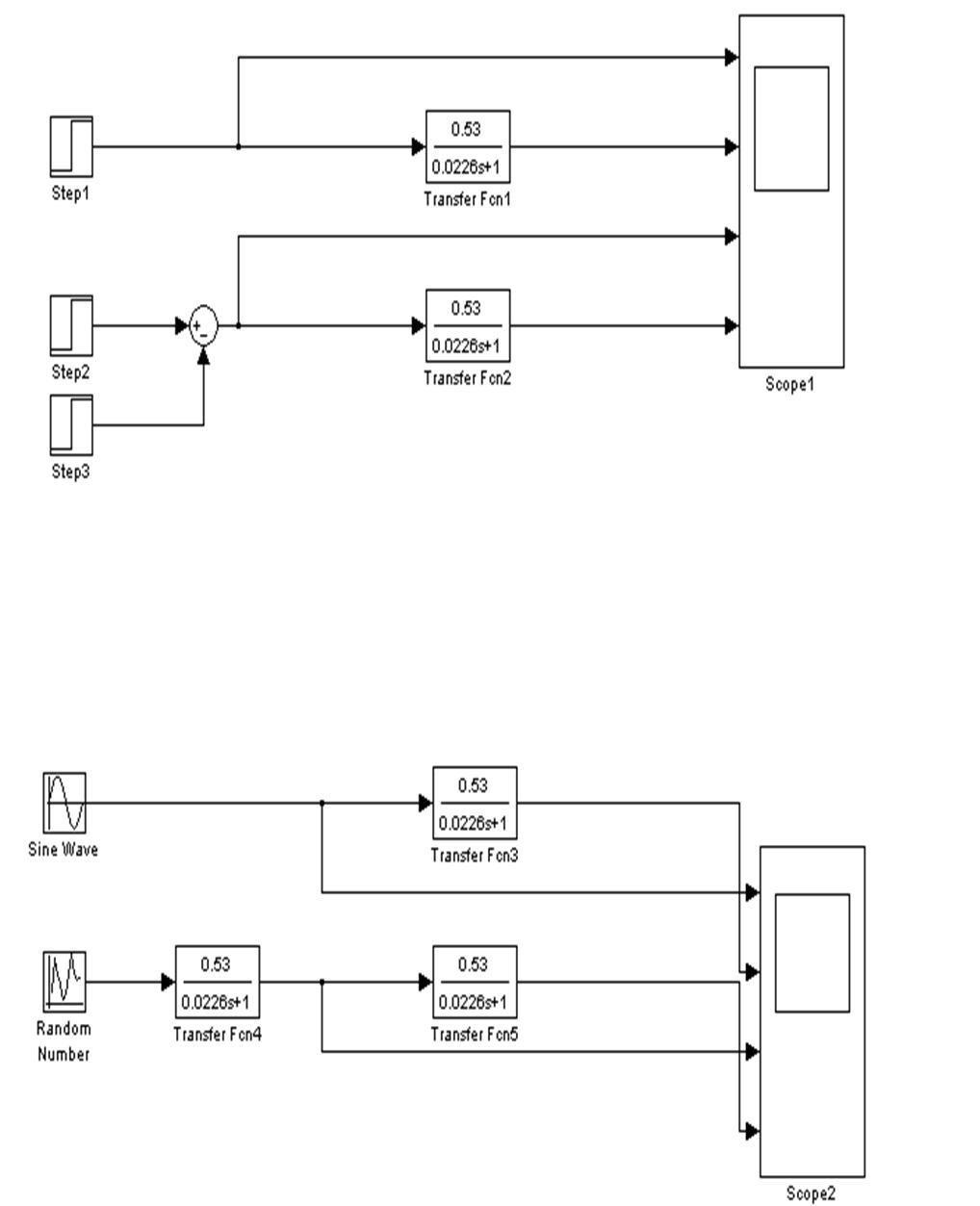
3.1. Találunk egy átviteli függvénye működtető csatorna „armatúrafeszültség - sebesség a meghajtó”
A hajtás lehet két részre osztható: az elektromos és mechanikus alkatrészek. Elektromos része által leírt Kirchhoff és mechanikai tehetetlenségi nyomatéka, és terhelési ellenállás.
Az egyenlet a mechanikai hozzátartozik:
ahol MDV - a motor tengelye
Ms - ellenállási nyomaték
Az egyenlet az elektromos motorok:
ahol ea - EMF az armatúra
- csak akkor van jelen, amikor az áram a forgórész
Ebben az esetben a tehetetlenség a rendszer határozza meg a tehetetlenségi nyomaték J. Ebben a tekintetben kevés idő tranziensek azonban = 0.
Írunk az egyenletrendszert az eltérések: