Inhomogén lineáris másodrendű differenciálegyenletek állandó együtthatós,
Lineáris inhomogén differenciálegyenlet (LNDU) a másodrendű állandó együtthatók formájában, ahol p és q - tetszőleges valós számok, és az f (x) - a folyamatos integrációs intervallum X.
Megfogalmazzuk a tétel, amely megmutatja a formát, amelyben egy olyan közös megoldást LNDU.
Az általános megoldás az intervallum X lineáris inhomogén differenciálegyenlet folyamatos intervallumon integráció X faktorral és a folytonos f (x) az összege az általános megoldás a megfelelő lineáris Közönséges differenciálegyenletek és különösebb oldatot az eredeti inhomogén egyenlet, azaz.
Így, az általános megoldás az inhomogén lineáris másodrendű differenciálegyenlet állandó együtthatók összege az oldat teljes a megfelelő másodrendű lineáris Közönséges differenciálegyenletek állandó együtthatók és saját megoldások kiindulási LNDU :. Ez van leírva a cikkben lineáris homogén másodrendű differenciálegyenletek állandó együtthatók, és továbbra is, hogy megtanulják felismerni.
Számos módszer megtalálására egy adott megoldás LNDU másodrendű állandó együtthatós. Módszerek függően választjuk formájában az f (x). A jobb oldali az egyenlet. Mi listát, és megvitassák megfelelő megoldásokat inhomogén lineáris másodrendű differenciálegyenletek állandó együtthatók.
Ha f (x) egy polinomiális n-ed-fokú az f (x) = Pn (x). LNDU majd az adott oldatot kérik formájában, ahol Qn (x) - a polinom foka n. és r - száma gyökerek karakterisztikus egyenlet egyenlő nullával. Mivel - egy adott egyenlet megoldása, a tényezők, amelyek meghatározzák a polinom Qn (x). Ez a módszer a meghatározatlan együtthatók az egyenlet.
Oldja meg a Cauchy probléma.
Más szóval, meg kell találni egy adott oldat inhomogén lineáris másodrendű differenciálegyenletek állandó együtthatók, amelyek megfelelnek a kezdeti feltételek.
Tudjuk, hogy az általános megoldás az inhomogén lineáris egyenlet összege az általános megoldás a megfelelő homogén egyenlet egy partikuláris megoldása az inhomogén egyenlet, hogy van.
Először is, találunk egy általános megoldást LNDU tovább a magánszektornak nyújtott hitelek döntést.
Found. Ehhez mi írjuk a karakterisztikus egyenlet és megtalálja a gyökereit.
A gyökerek a valós és a különböző, így.
Azt viszont, hogy. Mivel a jobb oldalán a kezdeti egyenlet a polinom másodfokú és egy gyökere a karakterisztikus egyenlet nulla, akkor az adott oldatot kérik formájában, ahol A, B és C - meghatározatlan együtthatók. Ezek a tényezők határozzák meg az egyenletet.
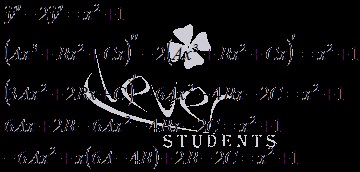
Egyenlővé együtthatók az azonos kitevők x. Eljutunk egy lineáris egyenletrendszer. Megoldása, hogy bármilyen módon (ha szükséges, lásd a cikk, megoldására rendszerek lineáris algebrai egyenletek), megkapjuk a szükséges meghatározatlan együtthatók. Következésképpen ,.
Ez egy általános megoldást az eredeti, nem-homogén lineáris másodrendű differenciálegyenletek állandó együtthatók.
Továbbra is megtalálni egy adott megoldás kielégíti a kezdeti feltételek. Ez azt jelenti, meg kell határoznia az ilyen C1 és C2 az egyenletben, hogy megfelel a feltételeknek.
Másrészt.
Így kapunk egy egyenletrendszer. Location.
Ezért a megoldás a Cauchy probléma a funkció
Ha az f (x) képviseli a termék a polinom foka n és a kitevő, majd az adott oldatot LNDU második kérelmei formájában, ahol Qn (x) - a polinom n-ed-fokú, R - a szám a gyökerek a karakterisztikus egyenlet egyenlő. A polinom együtthatóit Qn (x) a következő egyenletből meghatározzuk.