Ilyen megoldásokat
A grafikon az elektromos áramköri ábrán látható. 11, b. A grafikonon látható fa vastag vonallal.
Mivel a gráf sor fa ágai összeköti áramköri elemek, de nem zárt hurkot képeznek, akkor nyilvánvaló, hogy a fa ábrán látható. 11 b, ez nem egyedi.
A diákok arra ösztönzik, hogy a saját változatát más fák egy adott gráf.
Mátrix csatlakozások (csomópontok) lesz formájában:

Ez a mátrix van írva, hogy a K-1 csomópontok és láthatóan tehát nem az egyetlen lehetséges. Jegyezzük fel a mátrix, ha eltávolítják, például az 1. csomópont, vagy 2 perc.
Megadása az irányt az áramkör óramutató járásával megegyező irányban hurkok (ábra. 11, b), írunk a mátrix áramkör

Felvételkészítés Kirchhoff törvénye egyenletek igényelnek diagonális mátrix áramkör ellenállás:

Multiplikátorhatás vegyületek mátrix vektor-mátrix ág áramok


Ez egyenletek írt 1-jén Kirchhoff törvény.
Következő kontúrok mátrixot megszorozzuk a vektor-mátrix hangsúlyozza ágak

Vagy kap a következő egyenletet:

Tekintettel arra, hogy a

Ez az egyenlet írt a 2. Kirchhoff törvénye.
8. * A ábrán bemutatott áramkör. 11, egy, levelet az egyenletrendszert számító áramkör által a hurok áramok és a csomóponti potenciálok segítségével mátrix áramkörök és csatlakozások.
Kiszámításakor áramkör által használt csomóponti ágak vezetési diagonális mátrix:

Szorozzuk meg a mátrixot a mátrix vegyületeket konduktanciákat


Az eredmény egy mátrix csomóponti képességre.
Továbbá, a mátrix G megszorozzuk az y vektor mátrix csomópontok potenciálokat, és a vektor-mátrix ágak áramok áramforrások megszorozzuk a mátrix vegyületeket
, (*)
Követve a fenti megkapjuk

tolerálható


A rendszer egyenletek eljárás hurokáramok szükséges kontúrok mátrixot megszorozzuk a diagonális mátrix rezisztencia ágak


Kapott hurokimpedancia mátrixban.
Következő kontúrok mátrixot megszorozzuk a vektor-mátrix EMF források ágak
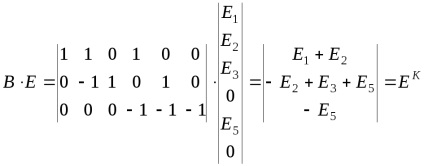
Az eredmény egy vektor-mátrix vázlat EMF.

- Kontúros ellenállás és az ellenállás között áramkörök
1.4. Módszer ekvivalens generátor.
9. * Határozzuk meg a leolvasott az áramkörben a 12. ábrán látható, és ha: R1 = 10 Ohm; R2 = 50Om; R3 = 40Om; R4 = 20Om; R5 = 20Om.
