Időközönként állandó jel funkció
Definíció 8. Az intervallum, amelyben a funkció tárolja egy bizonyos jel, az úgynevezett időközönként állandó jele a funkciót.
Nyilvánvaló, hogy a függvény grafikonját fölött fekszik az x-tengely, és amikor az alábbiakban, amikor a funkció előjelet, amikor áthalad a nullát vagy a megszakítási pont. A tartományban, ahol a függvény folytonos, és nincs nulla, annak jele van mentve.
2.7.1. Az algoritmus megtalálása időközönként állandó jel
1) Határozza meg a domain a funkció
2) Oldjuk egyenletet gyökerek, szerepelni fog a nullák.
3) a számegyenesen, hogy a domain a funkció és a nullák. A kapott időközönként, hogy meghatározzuk a jel funkciója.
4) Határozza meg időközönként állandó jel funkció.
Példa 2.5. Keresse meg a időközönként állandó jel funkció.
1. terület meghatározása a függvény
2. Tegyük az egyenlet megoldásához nullák vannak pontok
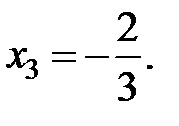
eredetét (azaz. e. egy vonalat, amely a görbe a grafikon kap tetszőlegesen közel). Megkülönböztetni függőleges, vízszintes és ferde aszimptota. Definíció 14. Azt mondják, hogy a vonal a függőleges aszimptotája a függvény grafikonját, ha (5.).
Tétel tétel 4. Közvetlen ferde aszimptőta függvény grafikonján (ábra. 5) akkor és csak akkor van véges korlátai
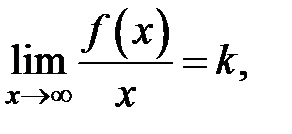
1. A definíció magában foglalja, hogy a függőleges aszimptóta kell nézni pontok diszkontinuitás a végtelen (a második fajta törés pont). Amikor közeledik a diszkontinuitás pont (legalább az egyik oldalán - bal vagy jobb) tart végtelenbe függvény grafikonját tetszőlegesen közel van egy egyenes vonal
2. A függvény grafikonját tetszőleges számú függőleges aszimptotákkal vagy nincs.
3. Annak megállapításához, a jelenléte a aszimptóta külön kellene határérték alatt, és ezzel kapcsolatban a funkció
- ugyanolyan ferde a asymptote (ábra6 a);
- különböző ferde asymptote át és (6. ábra, b).
-Have ferde asymptote csak akkor, vagy ha (ábra. 6c).
4. A speciális esete a ferde aszimptotákkal (at) egy vízszintes aszimptota. Direct vízszintes aszimptotája a grafikon egy időben, és csak akkor, ha
5. tartás funkció keresztezik ferde és gorizontalnoyasimptotami véges vagy végtelen számú pontot.
1) Határozza meg a domain a funkciót.
2) Határozzuk meg a jelenléte a második típusú töréspontokkal (lásd. 1. megjegyzés).
3) Az egyenlet, hogy megtalálják a ferde aszimptotákkal
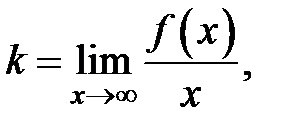
Példa Példa 2.7. Keresse meg a aszimptotája a grafikonon:
1) Határozza meg a domain a funkció
2) egyenletben függőleges aszimptotákkal óta
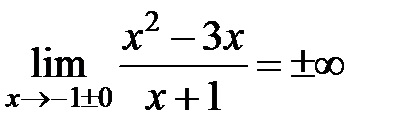
3) egyenletben ferde aszimptotákkal
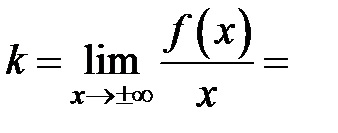
Így - ferde aszimptotája a grafikon funkciók.
2) - egy függőleges asymptote, mint
3) tisztázzák a kérdést, hogy a jelenléte egy ferde aszimptota meg, mert a funkció határozza meg csak
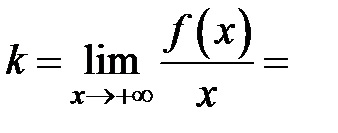
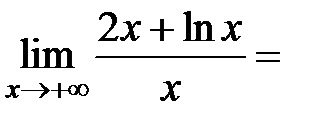
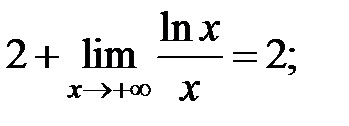
Következésképpen, a grafikon ennek a funkciónak nem hajlamos aszimptotákkal (lásd. 4. tétel).