Hogyan számoljuk ki a valószínűsége
A valószínűség statisztikai mérőszáma lehetőségeket. Miért statisztika? Mivel a gyakorlati szempontból, meg kell foglalkozni a sok (vagy készlet) az események, egy vagy több, amely bizonyos körülmények között még megfizethető, mint mások. Itt látható a „több” vagy „kevesebb, mint”, matematikailag kifejezhető - és van esély.

oktatás
Klasszikus képletű valószínűsége (Laplace-féle formula) az alábbiak szerint:
P (A) = M / N, ahol a
P (A) - a valószínűsége az esemény A
M - számú elemi események kedvező esemény egy
N - számú elemi sobytiy.Dva legegyszerűbb példa. Egy olyan helyzetben, essek egy érmét, ha kell számítani a valószínűsége „farok” (A esemény), kedvelt az esemény jelentése is. Ha kell számítani a valószínűsége, hogy a még oldalait a dobott kocka elősegíti elemi esemény lesz három (a eshetnek páros három). Ennek megfelelően, a valószínűsége egy esemény A 0.5 lesz, és az első és a második esetben.
Csak egy pár szót a lehetőségeket. Elméletileg a valószínűsége olyan esemény fog történni szükségszerűen, az úgynevezett „jelentős” (valószínűség egyenlő egység). A pontosság az ellenkezője - a „lehetetlen” esemény (a valószínűsége nulla). Egy esemény, ami történhet vagy nem történik meg, a továbbiakban: „véletlenszerű” (a valószínűsége, hogy egy véletlen esemény 0
Van egy másik definíciója a valószínűség (vagy pontosabban, a geometriai értelmezése a valószínűség): P (A) = Q / S, ahol a
S - területe a szám, amely véletlenszerűen dob pont
Q - része a terület az ábra S, amely megkapja a pontot.
P (A) - a valószínűsége, hogy véletlenül dobott pont azon a területen Q.
A klasszikus probléma geometriai valószínűség: adott egy négyzet, amelyben a beírt kör. A téren dobás tochku- valószínűsége, hogy csökkenni fog egy kört, ez az arány egy kör és egy négyzet alakú területet (lásd a megoldást. Az ábra).
Összehasonlítani a két vett minták azonos lakosság, vagy két különböző állapotait egy és ugyanazon népesség a Student-féle módszerrel. Használd, hogy kiszámítja a különbségek jelentősége, hogy van, hogy tudja-e, hogy megbízik a mérést tesz lehetővé.

oktatás
Annak érdekében, hogy válasszuk ki a megfelelő számításának képletét a megbízhatóság, meghatározza a minta méretét csoportok. Ha a mérések száma 30-nál nagyobb, mint egy csoport lenne tekinthető nagy. Így három lehetőség van: vagy egy kis csoport, mindkét csoport nagy, egy kis csoport, a második - nagy.
Ezen felül, akkor tudnia kell, hogy függő mérés az első csoport a második mérést. Ha minden egyes i-edik kiviteli alakja az első csoportot szemben i-edik megvalósítási módja szerint a második csoport, hívják őket egymástól függenek. Ha belüli eltérések a csoport lehet cserélni, az ilyen csoportok nevezzük csoportok páronként nazavisimo kiviteli alakok.
Összehasonlításképpen csoportok páronként-független variánsok (legalább az egyik közülük nagynak kell lennie), használja a képlet ábrán bemutatott. A képlet lesz képes megtalálni a Student kritérium, ez neki meghatározza a bizalom valószínűsége különbség a két csoport között.

Ahhoz, hogy meghatározzuk a t-teszt kisebb csoportok kölcsönösen független kiviteli alakokban, különböző képlet, ez képviseli a második képet. A számú szabadsági fokkal kell kiszámítani, ugyanúgy, mint az első esetben: szeres mennyisége a két minta és vonjuk ki a 2-es szám.
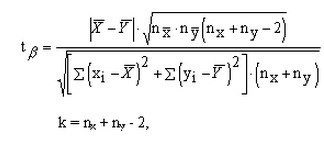
Hasonlítsa össze a két kis csoportok kölcsönösen függő eredmények felhasználásával két képlet közül lehet választani. A számú szabadsági fokkal számítjuk eltérően a képlet, k = 2 * (n-1).
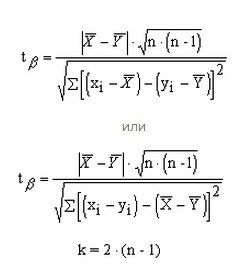
Ezután meghatározzuk a valószínűsége, hogy a bizalom az asztal Student t-teszt. Ebben az esetben vegye figyelembe, hogy a minta helyes volt, a megbízhatósági szint legyen legalább 95%. Ez azt jelenti, megtalálja az első oszlop a jelentősége szabadsági fok, és az első sorban - a számított t-próba és a szavazás kisebb vagy nagyobb, mint a kapott 95% -os valószínűséggel.
Például, ha van t = 2,3 k = 73. A táblázatból határozza meg a bizalom a valószínűsége, hogy 95% -nál nagyobb, ezért a különbségek jelentősek mintákat. Egy másik példa: t = 1,4- k = 70. A táblázat szerint, hogy megkapjuk a minimális megbízhatósági értékét 95%, k = 70, t kell egyenlőnek lennie legalább 1,98. Megcsinálta kevesebb - csak 1,4, így a különbség nem szignifikáns mintát.
Figyelem, csak ma!