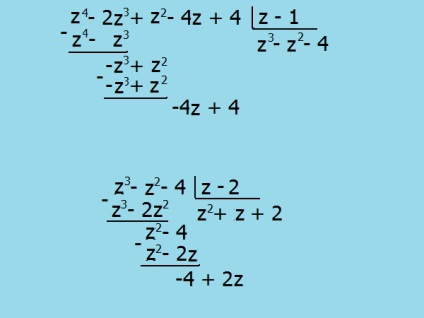Hogyan lehet megtalálni a közös tényező - vagyis a közös tényező - Matematika
Algebrai kifejezések van szükség számos területen a matematika, beleértve a döntés az egyenletek magasabb fok, differenciálódás és integráció. Ez többféle módszer, köztük faktoring. Ahhoz, hogy ezt a módszert, meg kell találni, és egy közös tényezőt ki a zárójelben.

A bevezetése közös tényező ki a zárójelben - az egyik leggyakoribb módja a faktoring. Ezt a technikát használják, hogy egyszerűsítse a szerkezet hosszú algebrai kifejezések, azaz polinomok. Közös tényező lehet egy szám, egy egytagú vagy kéttagú, és keresni alkalmazza a szorzás disztributív tulajdonság.
Chislo.Posmotrite óvatos az együtthatók mindegyik eleme egy polinom, tudjuk osztani őket ugyanazt a számot. 4 lesz • (3 • z³ + 4 • ZZ - 1) 4 nyilvánvaló tényező 4. Az átalakítás után - például az expressziós 12 • z³ + 16 • ZZ. Más szóval, ez a szám a legkisebb közös egész osztója minden együttható.
Odnochlen.Opredelite tartalmazzák-e ugyanazon változó az egyes kifejezéseket a polinom. Tegyük fel, hogy ez így van, most nézd meg a tényezőket, mint az előző esetben. 9. példa • z ^ 4 - 6 • z³ + 15 • ZZ - 3 • Z.
Minden egyes eleme a polinom tartalmaz egy variábilis z. Továbbá, minden együttható - többszörösei 3. Következésképpen, egy közös faktornak egytagú 3 • z: 3 • z • (3 • z³ - 2 • ZZ + 5 • Z - 1).
Dvuchlen.Za zárójelben kiszabott közös tényezője a két elem, és egy változó szám, amely egy olyan megoldás közös polinom. Ezért, ha -dvuchlen tényező nem egyértelmű, meg kell találni legalább egy gyökér. Kiemelés szabad kifejezés a polinom együtthatót nélkül változtatható. Most kell alkalmazni a helyettesítési módszer egy általános kifejezés az összes szerves osztója a konstans tag.
Vegyünk egy példát: z ^ 4 - 2 • z³ + ZZ - 4 • Z + 4. Ezután ellenőrizze, hogy bármely egész szám osztója 4 gyökere az egyenlet z ^ 4 - 2 • z³ + ZZ - 4 • Z + 4 = 0. egyszerű helyettesítés lokalizálják z1 = z2 = 1, és 2, ez azt jelenti, hogy a zárójelben lehet venni binomials (Z1) és (z2). Ahhoz, hogy megtalálja a többi kifejezés, a soros hosszú részlege.