hajlító deformáció - studopediya
Hajlító alakváltozás alatt azt értjük, hogy miként hatnak a külső erők a test, ami a változás görbület a test.
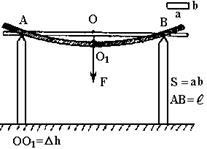
Ábra. Az 1. ábrán egy speciális esete a hajlító - keresztirányú hajlító a bárban nyugszik a támogatást. Span AB = l. Hajlítási F erő alkalmazása a bar az O pont (AO = OB). OO1 = Dh - lehajlás pont O. Hooke-törvény alkalmazása a keresztirányú hajlító alakváltozás felírható
ahol b - hajlítás tényező függvényében más tulajdonságai, mérete és alakja a bárban.
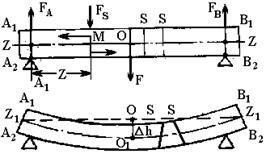
Amikor a hajlító alakváltozás a keresztrúd egyenes kezdetben bar ZZ tengelyre (ábra. 2) alatt az F erő ívelt, és a keresztmetszet S, egymással párhuzamosan hajlítás, S // S, elfordul egymáshoz képest. Felső bar A1 B1 szálak lerövidülnek, és az alsó A2 B2 - megnyúlt. A legnagyobb tömörítési fordul elő a legfelső szálak, és a legnagyobb a feszültség - a legalacsonyabb. A szálak úgy vannak elrendezve a Z1 Z1 tengelye hajlítva, de a hossza nem változik. Ez a réteg az úgynevezett semleges fázist. Így a keresztirányú törés a szálak az egyik oldalon valósul a Z tengely nyúlik, a másik - a tömörítés a hosszanti irányban (a Z tengely mentén) húzódik a szálak között váltani. (Elektromágneses kölcsönhatás atomok ad okot, hogy a rugalmas erők).
Bármely része a bár hajlítónyomaték M jár és keresztirányú (nyírás) erő FS. Amint az ábrából látható. 2, a hajlítónyomaték a keresztmetszete bizonyos távolságban A hordozó a parttól Z, egyenlő: M = FA Z (ez a képlet érvényes 0 £ Z £ l / 2), Nr FA = FB = F / 2, mivel a JSC feltétel = OB, így végül a hajlítónyomaték:
Általános képlet 3, a hajlítónyomaték változik egyik területről a másikra, és eléri a maximális értéket; O pont:
A nyíróerő FS teljes hosszában a sáv lesz állandó, és egyenlő:
bár lehajlás eléri a maximális értéket Dh O szakasz, ahol a maximális hajlító nyomaték jár Mmah.
A számítások azt mutatják, hogy a nagyságát a legnagyobb alakváltozás összefüggés adja meg:
ahol E - a rugalmassági modulus, Young modulus; J - tehetetlenségi nyomatéka a keresztmetszet a palló képest a központi tengellyel.
Abban az esetben, négyszögletes szakasza a deszka oldalú a és b. ahol a> b, a keresztmetszeti tehetetlenségi nyomaték egyenlő:
Behelyettesítve egyenlet (4) és (7) be (6) kapjuk:
ahol a húzási rugalmassági modulusa E határozzuk meg a keresztirányú hajlítási deformáció lenne: