gauss
Két rendszerek lineáris egyenletek úgynevezett egyenértékű. ha a beállított mindegyikük azonos megoldásokat.
Elemi transzformációk egy egyenletrendszer - jelentése:
- Törlése triviális egyenletrendszer, azaz azok, amelyekben minden együttható nulla;
- A szorzás bármely egyenlet számos nullától eltérő;
- Amellett, hogy bármely i-edik egyenlet bármilyen j -Ez egyenletet szorozva tetszőleges számú.
Változó xi úgynevezett szabad. Ha ezt a változót nem megengedett, és az egész rendszer egyenletek - megengedett.
Tétel. Elemi transzformációk alakítjuk ekvivalens egyenletrendszer.
Hogy mit jelent a Gauss módszer lényege, hogy megtérít az eredeti egyenletrendszert és kap az egyenértékű engedélyt vagy az ezzel egyenértékű inkompatibilis rendszer.
Tehát, Gauss módszer áll a következő lépéseket:
- Vegyük az első egyenletben. Válassza ki az első nem nulla együttható és felosztják a teljes egyenlet hozzá. Kapunk egy egyenlet, amelyben a változó xi tartozéka együttható 1;
- Kivonásával ez az egyenlet a többi, megszorozva az ilyen számokat, hogy az együtthatók változó xi fennmaradó egyenletek vissza. A rendszer használata engedélyezett a változó xi. és ekvivalens az eredeti;
- Ha triviális egyenlet (ritka, de például 0 = 0), és törölje őket a rendszerből. Ennek eredményeként egyenletek egyike lesz kevesebb;
- Ismételjük meg az előző lépéseket legfeljebb n-szer, ahol n - az első számú egyenletek a rendszerben. Minden alkalommal, amikor úgy döntünk, hogy a „feldolgozás” az új változó. Ha vannak ütköző egyenletek (például 0 = 8), a rendszer inkonzisztens.
Ennek eredményeként, néhány lépés után megkapjuk minden engedélyezési rendszer (esetleg szabad változók), vagy nem kompatibilis. Megengedett rendszer sorolhatók két esetben:
- A változók száma megegyezik a számát egyenletek. Ennélfogva, a rendszer meghatározott;
- A változók száma meghaladja a száma egyenletek. Mindezt szabad változók a jobb oldalon - kap egy képletet a megengedett változókat. Ezek a képletek és írásbeli vissza.
Ez az! A lineáris egyenletrendszer megoldódik! Ez egy meglehetősen egyszerű algoritmus, és annak fejlődését nem feltétlenül vonatkoznak a tutor a magasabb matematika. Vegyük ezt a példát:
Feladat. Problémák a egyenletrendszert:
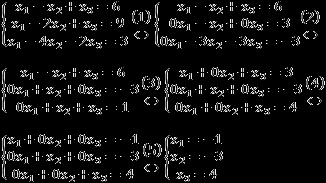
- Kivonjuk az első egyenletben a második és a harmadik - lehetővé változó x 1;
- Szorozzuk meg a második egyenletet (-1), és elosztjuk a harmadik egyenlet (3) - kapjuk két egyenlet, amelyben egy x változó 2 tartalmaz egy faktor 1;
- Mi adjuk hozzá a második egyenletben az első és a harmadik - kivonni. Engedélyének megszerzését változó x 2;
- Végül, kivonjuk a harmadik egyenlet az első - engedélyek beszerzése változó x 3;
- Kapunk jogosultsági rendszere, írja le a választ.
Az általános megoldás egy lineáris egyenletrendszer - ez egy új rendszer, amely egyenértékű az eredeti, amelyben minden változót kifejezve a megengedett ingyenes.
Ha szüksége lehet egy általános megoldás? Ha van, hogy kevesebb lépésben (k - hány egyenlet). Azonban, az okok, amelyek a folyamat véget ér egy lépésben l Fontos megérteni, hogy a megjelenése az ellentmondásos egyenlet Gauss módszer - ez ésszerűen összeférhetetlenséget. Ugyanakkor megjegyezzük, hogy ennek eredményeként az L-edik lépésben nem maradhat triviális egyenletek - ezek törlésre kerülnek közvetlenül a folyamatba. Feladat. Fedezze fel a kompatibilitás, és találni egy általános megoldást a rendszer: Tehát a rendszer inkonzisztens, mivel talált egy ellentmondásos egyenlet. Feladat. Fedezze fel a kompatibilitás, és találni egy általános megoldást a rendszer:
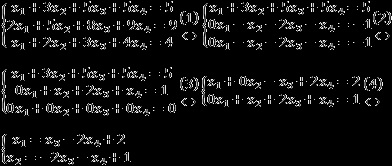
- Kivonjuk az első egyenletben a második (pre-kettővel megszorozva), és a harmadik - lehetővé változó x 1;
- Kivonva a második egyenletet a harmadik. Mivel minden együttható ezekben egyenletek ugyanazok, a harmadik egyenlet lesz triviális. Ugyanakkor a második egyenletet megszorozzuk a (-1);
- Vonjuk ki a második az első egyenletből - kap engedélyt változó x 2. A teljes egyenletrendszer most is megengedett;
- Mivel az x 3 és x 4 - állás, átadják a jogot arra, hogy kifejezze megengedett változókat. Ez a válasz.
Így, az illesztőrendszer és bizonytalan, mivel a két engedélyezett változó (x 1 és x 2), és a két szabad (x 3 és x 4).
- Munkavégzés képletek a probléma B12
- Összeadása és kivonása frakciók
- tétele Térség
- Általános rendszere megoldást B15 feladatok
- A legmagasabb és a legalacsonyabb érték
- Ingyenes Felkészülés a vizsgára 7 egyszerű, de nagyon hasznos tanulságokat + házi feladat
