Gauss-tétel, akkor a fizika
Kísérletileg meghatározott Coulomb-törvény és a szuperpozíció elve teljes mértékben leírja az elektrosztatikus tér egy adott rendszer díjak vákuum. Tulajdonságai azonban az elektrosztatikus tér ki lehet fejezni egy másik, általánosabb formában, anélkül, hogy a fogalom a Coulomb területén ponttöltés.
Bemutatjuk az új fizikai mennyiség jellemző elektromos mező - az áramlási φ elektromos mező vektort. A hely, ahol egy elektromos mező, egy kellően kis játszótér ds. A terméket a vektor modul területet δS és a koszinusza a szög α közötti a vektor és a normális, hogy a helyszínen nevezzük elemi folyam intenzitását vektor révén területen δS (ábra 1.3.1.):
ahol En - normál területen komponens modul
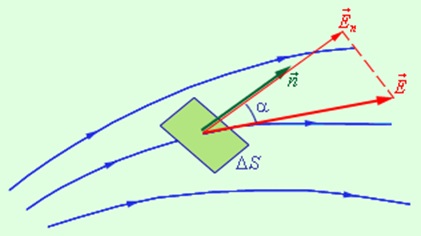
A definíció szerint egy elemi adatfolyam δφ
Nézzük néhány önkényes zárt felület S. Ha megszegjük a felszínen a kis területen δSi. azonosítani elemi folyamok δφi területen keresztül ezeket a kis területeken, és akkor összegezzük, az eredmény kapunk φ áramlási vektor a zárt S felület (ábra 1.3.2.):
Abban az esetben, egy zárt felület mindig választjuk a kifelé normális.
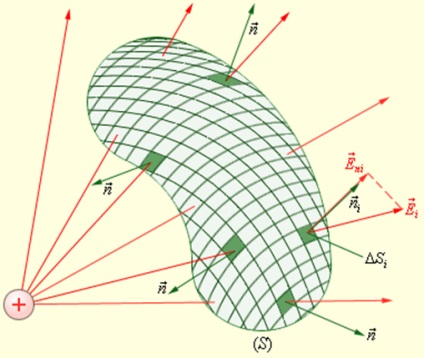
Kiszámítása fluxus F révén egy tetszőleges zárt felület S
Gauss-tétel kimondja:
Áramlási intenzitások vektor elektrosztatikus polyacherez tetszőleges zárt felület megegyezik az algebrai összege a díjak, belsejében található a felület osztva a villamos állandó ε0.
Ennek bizonyítására nézzük először azt a gömbfelület S. középpontja a töltés q. Az elektromos mező bármely pontján a gömb felületére merőleges, és egyenlő a modulo
ahol R - a gömb sugarának. Áramlási φ keresztül a gömb alakú felület megegyezik a termék terület egy gömb E 4πR 2. Következésképpen,
Most körülveszik ponttöltés tetszőleges zárt felület S és megvizsgálja támogatása sugarú gömb R0 (ábra. 1.3.3).
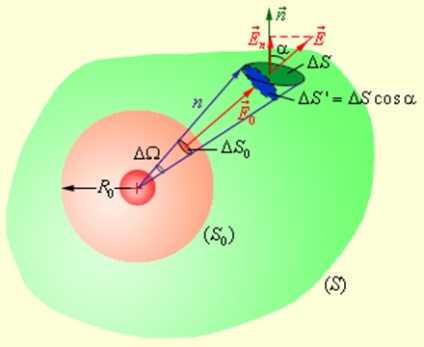
Betáplálási ponton az elektromos mező töltés bármilyen körülvevő felület töltés S.
Vegyünk egy kúp kis térszög a vertex δω. Ez a kúp osztja gömb kis területen δS0. és a felszínen S - területe δS. Elemi stream δφ0 és δφ ezeken a helyeken keresztül azonos. Tény, hogy
Ott δS „= δS cos α - piacon kiosztott kúpos szilárd szögben a sugarú gömb δω N felületre.
Ettől. egy, Ebből következik tehát, hogy a teljes elektromos fluxus révén egy tetszőleges ponttöltés felülete, csatolva a töltés, egyenlő a fluxus φ0 felszínén keresztül a járulékos területek:
Hasonlóképpen nem lehet bizonyítani, hogy ha egy zárt felület S nem tartalmaz egy pont q töltéssel. az adatfolyam φ = 0. Ilyen esetben ábrán mutatjuk be. 1.3.2. Valamennyi elektromos erővonalak ponttöltés áthatoljon a zárt felület S. Belül S felület a díjak nem, így ezen a területen a távvezeték nem törik le, és nem merülnek fel.
Általánosítása, a Gauss-tétel egy tetszőleges töltéseloszlásbeli ered szuperpozíció elve. Field bármilyen díj elosztása is képviselteti magát a vektor összege az elektromos mező pont díjakat. Φ díjak áramlási rendszer segítségével egy tetszőleges zárt felület S áll az áramlás φi elektromos mezők az egyes díjakat. Ha a töltés qi S. felülete volt, benne hozzájárul a fluxus egyenlő, ha ez a töltés van kapcsolva külső felületén, majd a hozzájárulása a villamos mező fluxust egyenlő nullával.
Így a Gauss-tétel.
Gauss-tétel következménye Coulomb-törvény és a szuperpozíció elve. De ha elfogadja a nyilatkozatot a jelen tétel a kezdeti axióma, akkor ez annak a következménye, Coulomb-törvény. Ezért Gauss-tétel néha alternatív megfogalmazása Coulomb-törvény.
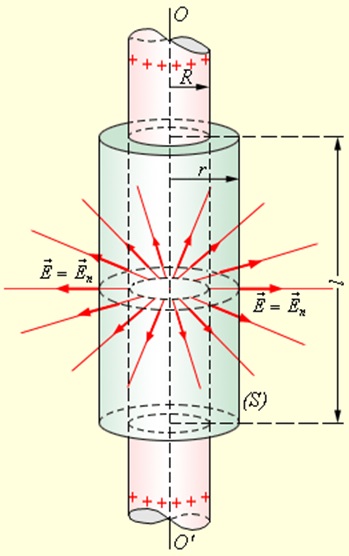
A Gauss-tétel, lehetséges bizonyos esetekben, hogy könnyen kiszámítható az elektromos mező körül a töltött test, mivel ha a töltés eloszlás szimmetriáját és a teljes szerkezetét a mező előre kitalálni.
Egy példa a probléma számítási területen vékony falú, üreges egyenletesen töltött hosszú henger R sugarú Ez a célkitűzés tengelyszimmetrikus. A szimmetria alapján, az elektromos mező kell sugárirányban. Ezért, hogy alkalmazni Gauss-tétel célszerű választani egy zárt felület S formájában koaxiális henger R sugarú és L hosszúságú. mindkét végén zárt (ábra. 1.3.4).